Фурье в наименьших квадратах

[zgemm]

Добрый день,

помогите, пожалуйста, разобраться с Фурье в наименьших квадратах, для двух функций $c(t), f(t)$ которые бесконечно затухают к обеим границам определения $[-T,T]$ мне надо преобразовать задачу минимизации

$$\min_{a_n, d_n} \int_{-T}^T ||c(t) - \sum_{n=1}^N a_n f_n(t + d_n) ||_2^2 dt ~~~~~~ (1)$$

в спектральную область, то есть применив

$$z(x) = \frac{1}{2\pi}\int c(t) e^{-tx} dx$$

$$g(x) = \frac{1}{2\pi}\int g(t) e^{-tx} dx$$

получить что-то вроде

$$\min_{a_n, d_n} \int_{-X}^X ||z(x) - \sum_{n=1}^N a_n g_n(x) e^{x d_n} ||_2^2 dx ~~~~~~ (2)$$

Я запутался, на матричном уровне через матрицы сдвига и их циркулянтные свойства тут вроде все верно, а на интегральном не могу по шагам это расписать, затыкаясь на том, что после подстановки

$$\min_{a_n, d_n} \int_{-T}^T \int z(x_1) e^{x_1 t} - \sum_{n=1}^N a_n g_n(x_1) e^{x_1 (t + d_n)} dx_1 \int z(x_2) e^{x_2 t} - \sum_{n=1}^N a_n g_n(x_2) e^{x_2 (t + d_n)} dx_2 dt$$

не понимаю, как далее перейти к (2), помогите, пожалуйста, в этом по шагам разобраться.

Спасибо!!!

[drzewo]

Очередной безграмотный текст от ТС.

zgemm в сообщении #1679978 писал(а):

Фурье в наименьших квадратах

это новый термин такой, и что он значит?

zgemm в сообщении #1679978 писал(а):

и

$$\min_{a_n, d_n} \int_{-T}^T ||c(t) - \sum_{n=1}^N a_n f_n(t + d_n) ||_2^2 dt ~~~~~~ (1)$$

$\|\cdot\|_2$ -- это собственно что? если $L^2-$ норма чего-то там, то от $t$ эта норма зависеть стало быть уже не должна. От чего мы тогда считаем $\int_{-T}^T$? И откуда взялась последовательность функций $f_n$? Выше про нее сказано не было.
Каковы свойства функций?

zgemm в сообщении #1679978 писал(а):

менив

$$z(x) = \frac{1}{2\pi}\int c(t) e^{-tx} dx$$

Интеграл берется по $x$ т.е. функцию от $t$ выносим за интеграл интегрируем экспоненту.
Можно было бы заподозрить преобразование Фурье с опечаткой -- но тоже не получается: выше сказано, что функция $c(t)$ определена на $[-T,T]$:

zgemm в сообщении #1679978 писал(а):

функций $c(t), f(t)$ которые бесконечно затухают к обеим границам определения $[-T,T]$

(граница определения -- это што?)

а для преобразования Фурье она должна быть определена на $\mathbb{R}$.
И т.д.

[Евгений Машеров]

Не совсем понял, Ваши функции периодические с периодом $2T$ или просто определены на $[-T, T]$?
Во втором случае - чем Вам поможет "фурьеризм" для сдвигов?

[zgemm]

Соглашусь, что много описок, очень прошу прощения, не в тех очках набивал и копировал, а сами формулы до сих пор предпочитаю ручкой на бумаге писать.

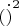
С $|| \dot ||_2^2$ - для восприятия надо было конечно $( \dot )^2$, но такое написание вызвано тем, что моя исходная задача как раз еще переменную имеет, в которой эта норма и применялась, очень прошу прощения, что ввел в заблуждение. С другой стороны, вектор из одного элемента, к которому применена $|| \dot ||_2^2$ дает именно то, что надо, так что формально я прав, просто написал заумнее, чем уважаемый drzewo хотел видеть.

С

$$z(x) = \frac{1}{2\pi}\int c(t) e^{-tx} d{\bf t}$$

$$g_n(x) = \frac{1}{2\pi}\int f_n(t) e^{-tx} d{\bf t}$$

именно описки, при копировании, как я говорил, не увидел, что символ не поправил, жалко, что drzewo так на меня взерошился, причем не в первый раз... Реально не понимаю, почему он так на меня реагирует :(

-- 26.03.2025, 16:12 --

Евгений Машеров в сообщении #1679996 писал(а):

Не совсем понял, Ваши функции периодические с периодом $2T$ или просто определены на $[-T, T]$?
Во втором случае - чем Вам поможет "фурьеризм" для сдвигов?

Функции не периодические, но они стремяться к нулю на концах отрезка. Можно их далее за границы отрезка продолжить на бесконечность, положив тождественно нулю. Небольшие сдвиги, возникающие от $d_n$ позволяют применять Фурье.

EDIT:

по поводу самих функций $c$, $f_n$. Верно, что надо дефинировать их от минус до плюс бесконечности, с ненулевым носителем в $[-T,T]$, и в дополнении я только могу сказать, что $f_n$ - нормированы (но не ортогональные), а норма $c$ ограничена сверху. Разрывы могут иметь место быть, число их ограничено небольшой константой. В первом приближении можно даже положить, что разрывов нет.