Определение перемещения при изгибе кольца.

[Georgiy7438]

Здравствуйте. Разбирая решение задачи по определению перемещения кольца при его изгибе из книги Л.И. Балабуха «Строительная механика ракет», я столкнулся с непонятным математическим приемом.
Требуется рассмотреть деформацию кольца под действием внешней нагрузки. Нагрузка считается определенной в виде функции изгибающего момента, возникающего в каждом сечении кольца.
Деформация определяется в виде трех функций: смещение точек кольца в касательном направлении ($\upsilon$), радиальном направлении ($\omega$) и поворот касательной ($\theta$) для каждой точки вдоль длины кольца. Каждая из функций зависит от угловой координаты $\varphi$ кольца. Для определения этих функций имеется следующая система дифференциальных уравнений:
$\frac{d^3}{d\varphi^3}\upsilon+\frac{d}{d\varphi}\upsilon=-\frac{R^2}{EI}\cdot M$
$\omega=\frac{d}{d\varphi}\upsilon$(1)
$\theta=-\frac{1}{R}\cdot (\frac{d^2}{d\varphi^2}\upsilon+\upsilon)$

В общем виде решение этих уравнений представляется в виде:
$\upsilon=\upsilon^*+C_0+C_1\cos\varphi+C_2\sin\varphi$
$\omega=-\frac{d}{d\varphi}\upsilon^*+C_1\sin\varphi-C_2\cos\varphi$(4)
$\theta=-\frac{1}{R}\cdot (\frac{d^2}{d\varphi^2}\upsilon^*+\upsilon^*)-\frac{C_0}{R}$

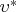
Где, $\upsilon^*$ - частное решение неоднородного дифференциального уравнения.

Вместе с этим, смещения точек кольца также могут возникать вследствие перемещения и поворота кольца как жесткого тела без его деформации, относительно системы координат, в которой рассматривается перемещения точек кольца. Функции, определяющие смещения и поворот точек кольца, вследствие перемещения кольца как жесткого тела выглядят так:
$\upsilon=a_0+a_1\cos\varphi-a_2\sin\varphi$
$\omega=a_1\sin\varphi-a_2\cos\varphi$ (3)
$\theta=-\frac{a_0}{R}$

Эти функции совпадают с функциями (2), с точностью до частного решения ДУ. Определить константы интегрирования уравнений (2) из условия периодичности не представляется возможным. Следовательно, требуется метод для разделения этих функций, в том случае, когда рассматривается одновременно деформированное кольцо и смещенное относительно системы координат произвольным образом. В таком случае, общее смещение представляется следующим образом:
$\upsilon=\upsilon^*+(C_0+a_0)+(C_1+a_1)\cos\varphi+(C_2-a_2)\sin\varphi$
$\omega=-\frac{d}{d\varphi}\upsilon^*+(C_1+a_1)\sin\varphi-(C_2+a_2)\cos\varphi$(2)
$\theta=-\frac{1}{R}\cdot (\frac{d^2}{d\varphi^2}\upsilon^*+\upsilon^*)-(\frac{C_0}{R}+\frac{a_0}{R})$
Где, константы $a_0, a_1, a_2$ – определяют смещение кольца как жесткого тела, а $C_0, C_1, C_2$ - константы интегрирования уравнения (2), которые определяют форму деформации кольца и зависят от функции момента М$(\varphi)$.

Затем, автор метода делает следующее. Он утверждает, что скалярное произведение функций (2) и (3) должно быть равно нулю для любого смещения кольца как жесткого тела (т.е. при любом значении и их сочетании между собой параметров а). Скалярное произведение определяется как интеграл произведения двух функций, вдоль всей длины кольца (угловая координата от 0 до $2\pi$). Исходя из этого требования выделяются единственные константы для уравнения (2), которые определяют действительную деформацию кольца.
Именно этот прием мне остался непонятен. Почему функции (2) и (3) должны быть ортогональны исходя из физического смысла задачи?  Есть ли физические основания, исходя из которых с помощью этого метода получается действительно именно та деформация, которая будет наблюдаться при приложении нагрузки к кольцу?

Далее приведу свои общие (и не вполне строгие) соображения. Общее смещение точек кольца есть сумма функций (2), (3), которые являются базисными. То есть каждая функция определяет смещение либо из-за деформации, либо от перемещения без деформации независимо от другой функции. Базисные функции должны быть ортогональны и условием ортогональности является равенство нулю скалярного произведения двух этих функций. Но как это совмещается с физическим смыслом решаемой задачи мне не ясно.

Несколько позже я заметил еще кое-что. Автор книги как следствие из условия ортогональности приводит следующие интегральные условия, которым должны удовлетворять функции, описывающие деформацию:

$$\int\limits_{0}^{2\pi}\upsilon d\varphi=0$$

$$\int\limits_{0}^{2\pi}\upsilon \sin\varphi d\varphi=0$$

$$\int\limits_{0}^{2\pi}\upsilon \cos\varphi d\varphi=0$$

$$\int\limits_{0}^{2\pi}\omega d\varphi=0$$

$$\int\limits_{0}^{2\pi}\omega \sin\varphi d\varphi=0$$

$$\int\limits_{0}^{2\pi}\omega \cos\varphi d\varphi=0$$

$$\int\limits_{0}^{2\pi}\theta d\varphi=0$$

В других книгах, где рассматривается та же задача (например: Образцов «Строительная механика летательных аппаратов» или Кан «Строительная механика оболочек») некоторые из этих интегральных условий подаются как факт (без разъяснения откуда они взялись) и с их помощью находятся постоянные интегрирования без прибегания к вышеупомянутой ортогональности. Но опять-же я не могу понять физический смысл этих интегральных условий. Прошу помощи у форума.