Косинус суммы и разности

[Mihr]

Этот вопрос, вроде бы, исчез из школьных учебников. И теперь соответствующие тождества даются без вывода. Между тем вывод этих тождеств (по крайней мере, для острых углов) совсем не сложен. И ещё находятся школьники, спрашивающие, откуда берутся эти тождества. Я объясняю так.

Вложение:

362.png

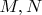
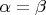
Возьмём единичную окружность и отложим от положительного направления оси абсцисс углы $\alpha$ и $\beta$ в разные стороны. Получим (на пересечении с окружностью) точки $M, N$. На отрезке $MN$, как на гипотенузе, построим прямоугольный треугольник $MKN$ с катетами, параллельными координатным осям (случай, когда $\alpha = \beta$, и треугольник вырождается в отрезок, можно рассмотреть отдельно, никаких сложностей этот случай не представляет). Запишем теперь выражение для $MN^2$ два раза:
1. Из треугольника $OMN$ по теореме косинусов

$$MN^2=1^2+1^2-2\cdot1\cdot1\cdot\cos (\alpha + \beta)$$

2. Из прямоугольного треугольника $KMN$ по теореме Пифагора

$$MN^2=NK^2+KM^2=(\cos \beta - \cos \alpha)^2+(\sin \alpha + \sin \beta)^2$$

Приравниваем правые части полученных равенств, раскрываем скобки и, используя основное тригонометрическое тождество, получаем нужное утверждение.
Выражение для косинуса разности можно получить отсюда же, заменив $\beta$ на $-\beta$ (только потребуется предварительно доказать чётность косинуса и нечётность синуса). Можно получить его и непосредственно из аналогичного рисунка. Просто углы $\alpha$ и $\beta$ в этом случае придётся отложить в одном направлении от оси абсцисс (а не в противоположных направлениях).

[drzewo]

$u=(\cos\alpha,\sin\alpha),\quad v=(\cos\beta,\sin\beta)\Longrightarrow$

$$\langle u,v\rangle=\cos(\alpha-\beta)=\cos\alpha \cos\beta+\sin\alpha \sin\beta$$

-- 21.01.2025, 02:30 --

Mihr в сообщении #1670912 писал(а):

Этот вопрос, вроде бы, исчез из школьных учебников.

Это может и правильно. Тригонометрии по моим воспоминаниям и так было многовато. Просто фетиш какой-то. Не говоря о том, что до полной строгости это все равно не довести в школе.

[Mihr]

drzewo, я говорил о доказательстве для школьника. По моему впечатлению, большинство школьников предпочитает опираться на ясные, наглядные образы. Вот я и стремился не к краткости, а к максимальной наглядности.

[drzewo]

Mihr в сообщении #1670915 писал(а):

я говорил о доказательстве для школьника

а что не так с доказательством через скалярное произведение?

[mihaild]

drzewo в сообщении #1670916 писал(а):

а что не так с доказательством через скалярное произведение?

А как доказать, что dot product это произведение длин на косинус?
Если косинус определяется геометрически (что и происходит в школе), то нам в любом случае придется какие-то нетривиальные геометрические соображения использовать прежде чем получить формулы.

[Mihr]

drzewo в сообщении #1670916 писал(а):

а что не так с доказательством через скалярное произведение?

Да всё так. Изящнее, спору нет. Но многие школьники скалярное произведение плохо воспринимают, "не чувствуют". Это кажется странным, но если поработаете со "средними" школьниками - не слушателями физматшкол, - думаю, убедитесь сами. Да и по-хорошему свойства скалярного произведения, в частности, его линейность - а отсюда формулу для вычисления скалярного произведения через координаты сомножителей - тоже ведь нужно обосновать. Если это обоснование включить в Ваш вывод, окажется ли он короче моего?

[drzewo]

mihaild в сообщении #1670917 писал(а):

А как доказать, что dot product это произведение длин на косинус?

Когда я учил школобесов то делал так.
Скалярное произведение по определению это $(\boldsymbol u,\boldsymbol v):=|\boldsymbol u|\cdot|\boldsymbol v|\cos\alpha$.
Потом доказываем билинейность скалярного произведения. Нетривиальной является только проверка свойства
$(\boldsymbol u+\boldsymbol v,\boldsymbol w)=(\boldsymbol u,\boldsymbol w)+(\boldsymbol v,\boldsymbol w)$

[Padawan]

drzewo в сообщении #1670914 писал(а):

$u=(\cos\alpha,\sin\alpha),\quad v=(\cos\beta,\sin\beta)\Longrightarrow$

$$\langle u,v\rangle=\cos(\alpha-\beta)=\cos\alpha \cos\beta+\sin\alpha \sin\beta$$

У меня в школе так и выводили.

-- Ср янв 22, 2025 13:09:13 --

drzewo в сообщении #1670919 писал(а):

Нетривиальной является только проверка свойства
$(\boldsymbol u+\boldsymbol v,\boldsymbol w)=(\boldsymbol u,\boldsymbol w)+(\boldsymbol v,\boldsymbol w)$

В учебнике Атанасяна насколькр я помню объясняется, что $(\boldsymbol u,\boldsymbol w)$ - это алгебраическое (т.е. с учетом знака) значение проекции вектора $\boldsymbol u$ на направление вектора $\boldsymbol w$, умноженное на $|\boldsymbol w |$. В вузовских учебниках по аналитической геометрии -- также.

А вот в теме про векторное произведение задумался, как выводится формула в координатах, там тоже самое сложное доказать свойство $[\boldsymbol u+\boldsymbol v,\boldsymbol w]=[\boldsymbol u,\boldsymbol w]+[\boldsymbol v,\boldsymbol w]$. Ну и вспомнил из термеха"правило Жуковского" (ЕМНИП): $[\boldsymbol a, \boldsymbol x]$ получится, если ортогонально спроектировать вектор $\boldsymbol x$ на плоскость, перпендикулярную вектору $\boldsymbol a$ и повернуть на $90$ градусов против часовоц стрелки.

[amon]

Padawan в сообщении #1671052 писал(а):

А вот в теме про векторное произведение задумался, как выводится формула в координатах, там тоже самое сложное доказать свойство $[\boldsymbol u+\boldsymbol v,\boldsymbol w]=[\boldsymbol u,\boldsymbol w]+[\boldsymbol v,\boldsymbol w]$.

Извиняюсь, что в чужой огород лезу. А чем $[\boldsymbol u,\boldsymbol w]_i=\varepsilon_{ijk}\boldsymbol{u}_j\boldsymbol{w}_k$ не устраивает?

[Padawan]

amon в сообщении #1671215 писал(а):

$[\boldsymbol u,\boldsymbol w]_i=\varepsilon_{ijk}\boldsymbol{u}_j\boldsymbol{w}_k$

Так это и есть формула в координатах. Как ее получить из геометрического определения векторного произведения?

[amon]

Padawan в сообщении #1671217 писал(а):

Как ее получить из геометрического определения векторного произведения?

На уровне школьников, или студентов? На уровне студентов, IMHO, проще всего - из того, что объем параллелепипеда это определитель, а этот объем равен $V=(\mathbf{a},[\mathbf{b},\mathbf{c}]).$ На уровне школьников - не знаю.

[drzewo]

amon в сообщении #1671225 писал(а):

На уровне школьников, или студентов?

Это одна из многочисленный дискуссий о том как преподавать математику в школе так что бы было и понятно и строго и соответствовало современному пониманию.
Хотя на мой вкус больше смысла в жанре литературы, который открыл Феликс Клейн: <<Элементарная математика с точки зрения высшей>>

-- 23.01.2025, 23:20 --

По-моему, гораздо важне не то как скормить школьнику формулу косинуса суммы, а что бы студент-математик понимал ее природу, групповую в частности.

[EUgeneUS]

Как выводилась формула в школе я не помню.
Но помню, как её запоминал - через формулу косинуса двойного угла. Вот такие костылики и реверсал инжиниринг.

Вывод через скалярное произведение - красивое.

[Combat Zone]

Padawan в сообщении #1671052 писал(а):

У меня в школе так и выводили.

Это не только у вас )
Через скалярное произведение доказательство было в обычном учебнике 8 класса по алгебре (10-летней средней школы). Например, Макарычев (1988), более ранних тоже. Может, я недооцениваю сложности, но тогда оно каких-то проблем не вызывало. Сейчас вообще все может быть.

[EUgeneUS]

Combat Zone в сообщении #1671370 писал(а):

Через скалярное произведение доказательство было в обычном учебнике 8 класса по алгебре (10-летней средней школы). Например, Макарычев (1988), более ранних тоже.

В середине 80-х в средней во всех отношениях школе.
"Тригнометрия", как раздел, где учат тригнометрческие тождества и решают кучу задач по ним - это первая четверть 9-го класса.