Неравенства 12-й степени

[Rak so dna]

Для действительных $a,b,c$ доказать:

$27\left(a+b\right)^4\left(b+c\right)^4\left(c+a\right)^4 \geq 64\left(ab+bc+ca\right)^3\left(a-b\right)^2\left(b-c\right)^2\left(c-a\right)^2$

[Rak so dna]

ForeverHaibara@AoPS нашёл красивое доказательство:

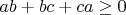
Для $ab+bc+ca<0$ очевидно. Для $ab+bc+ca \geq0$ имеем:

\begin{align*} &\sum{(a-b)^2}\cdot\left(27\prod(a+b)^4-64\left(\sum ab\right)^3\left(\prod (a-b)^2+\prod (a+b)^2\right)\right)\\ &=\sum {\left(b+c\right)^4\left(b-c\right)^2\left(ab+bc+ca-3a^2\right)^2\Bigl( \left(5(ab+bc+ca)+a^2\right)^2+2(a+b)^2(a+c)^2\Bigr)}\\ &+256\left(ab+bc+ca\right)^4\prod{(a-b)^2} \end{align*}

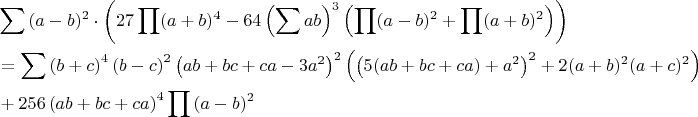
(code)

(a-b)^2*(a+b)^4*(2*(a+c)^2*(b+c)^2+(5*a*b+5*a*c+5*b*c+c^2)^2)*(a*b+a*c+b*c-3*c^2)^2+256*(a-b)^2*(a-c)^2*(b-c)^2*(a*b+a*c+b*c)^4+(a-c)^2*(a+c)^4*(2*(a+b)^2*(b+c)^2+(5*a*b+5*a*c+b^2+5*b*c)^2)*(a*b+a*c-3*b^2+b*c)^2+(b-c)^2*(b+c)^4*(2*(a+b)^2*(a+c)^2+(a^2+5*a*b+5*a*c+5*b*c)^2)*(-3*a^2+a*b+a*c+b*c)^2