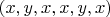кограницы и "ориентации"

[Nartu]

Здравствуйте.

Уже какое-то время я решаю некоторую задачу, приводящую к вычислению ко-граничного скрещеного гомоморфизма, как мне тут подсказали когда-то.
Написав программу, я заметил необычное для меня свойство решений, которое не могу объяснить (полностью). Цель обсуждения - найти объяснение.

И так, сама задача

Есть пространство $\mathbb{R}^n$ и циклическая группа$(\mathbb{Z}/n)$, действующая на компонентах его векторов циклическими перествановками. Рассмотрим кограничный скрещеный гомоморфизм из этого пространства на $\mathbb{R}^{n-1}$ :

$$h_{\sigma}:\mathbb{R}^n \to \mathbb{R}^{n-1}$$

Если $v \in \mathbb{R}^n$ то $h_{\sigma}(v)= p(\sigma v)-p(v)$

Где $\sigma$ будет указывать, какая перестановка(это будет целое число(остаток)), а $p \in \mathbb{R}^{n-1}$ и если $v=(x_1,\; x_2,\; \dots,x_n)$, то $p(v)=(x_1,\; x_1+x_2,\; x_1+x_2+x_3,\; \dots, \; x_1+ \dots +x_{n-1})$.
Действие указано до взятия $p$ что бы подчеркнуть, как оно работает. (Несложно понять, что $\sigma$ и $p$ коммутируют.)

Теперь я вычисляю $h_{\sigma}(v)$ для каждой перестановки, получив образ всей орбиты $v$.

Условие: Нужно, что бы каждая кограница в этом образе имела компоненты либо не больше нуля, либо не меньше. Иначе говоря - каждая перестановка даёт вектор без компонент разных знаков: либо все плюс либо минус. Нулевые можно.
Такая себе "ориентация", хотя так это называть может вызвать конфуз. Предлагаю просто распространять знак ненулевых компонент на весь вектор, если обладает этим свойством.

Цель — найти такие векторы $v$.
Обратите внимание — весь образ орбиты не обязательно одного знака! Каждый вектор из него может быть "ориентирован" индивидуально.

Раньше я не хотел подставлять значения, а сравнивать линейные комбинации компонент вектора(образа) по какому-то неплохому линейному порядку.
Это было обусловлено тем, что когда у начального вектора больше двух разных компонент, нельзя сделать вывод о знаке суммы его переменных компонент исходя из их сравнения.
Если две разных координаты, то всё просто: $y-x>0$, если $y>x$ и подставлять ничего не надо.
Мне тут подсказали взять лексический порядок, и я сразу пошел писать код. В результате получил какие-то примеры решений с даным числом разных компонент..

При попытке вычислить образ орбиты для проверки, оказалось, что кроме "двумерного" случая Все кограницы были одного знака. Никто не был другой "ориентации" !
А когда было лишь два значения координат, то иногда часть образа орбиты $v$ была другого "знака".

Мне удалось объяснить, почему начиная с решений для $v$ с тремя(и больше) разными компонентами у меня всё было в "одну сторону".
Для этого достаточно посмотреть на символьный вид всех кограниц, когда $v=(x_1,\; x_2,\; \dots,x_n)$. Об этом ниже

Зафиксируем размерность, на пример, $n=6$, получаем :

\begin{align*} &h_{1}(v)=(x_2 - x_1, \qquad\quad x_3 - x_1, \qquad\qquad\qquad\quad\quad x_4 - x_1, \qquad\qquad\qquad\quad\;\;\, x_5 - x_1, \quad\quad\quad\, x_6 - x_1)\\ &h_{2}(v)=(x_3 - x_1, \quad x_3 + x_4 - x_1 - x_2, \quad\qquad x_4 + x_5 - x_1 - x_2, \qquad\quad\;\, x_5 + x_6 - x_1 - x_2, \quad x_6 - x_2)\\ &h_{3}(v)=(x_4 - x_1, \quad x_4 + x_5 - x_1 - x_2, \quad x_4 + x_5 + x_6 - x_1 - x_2 - x_3, \quad x_5 + x_6 - x_2 - x_3, \quad x_6 - x_3)\\ &h_{4}(v)=(x_5 - x_1, \quad x_5 + x_6 - x_1 - x_2, \quad\qquad x_5+x_6 - x_2 - x_3, \qquad\quad\;\, x_5 + x_6 - x_3 - x_4, \quad x_6 - x_4)\\ &h_{5}(v)=(x_6 - x_1, \qquad\quad x_6 - x_2, \qquad\qquad\qquad\quad\quad x_6 - x_3, \qquad\qquad\qquad\quad\;\;\, x_6 - x_4, \quad\quad\quad\, x_6 - x_5)\\ \end{align*}

(Я пропустил $h_{0}(v)$ так как это всегда просто 0-вектор, и он ни на что не влияет.)

Тут много общих компонент. Если пригледеться, можно заметить, что у каждого вектора(образа) есть общая компонента с каждым другим! В иных размерностях должно быть так же...
Сразу напрашивается представлять это в виде полного графа. Условие задачи никак не связано с порядком координат, а значит, кограницы-векторы можно перевести в мультимножества.
Тогда граф будет графом пересечений мультимножеств, что уже стандартный термин.

Но тогда, если хоть одно ребро положительно, то его вершины положительны, а значит и все остальные их рёбра тоже.. "Цвет" знака распространяется всюду, где есть хоть одно "некрашеное" ребро.
Так что, для того, что бы были вершины противоположного знака, они должны быть изолированы от остальных — граф должен быть несвязным.
То есть, надо убить рёбра, а значит, — обнулить нужные компоненты.

А это — невозможно! если использовать сравнение сум переменных по лексическому порядку. Тогда нулём может быть только 0-вектор, и никто больше.
По крайней мере, тут должно быть достаточно ненулевых (общих) компонент в кограницах, что бы тот граф был связным, а значит, всегда полностью весь был положительным/отрицательным.

Наконец, я подошел к теме обсуждения.

Что бы искать случаи наличия разных "ориентаций" среди кограниц, можно обойтись без всякого лексического порядка, просто напрямую приравнивать к нулю общие координаты, что бы разбить тот граф на 2 и больше компонент связности.
Обязательно следить за выполнением основного условия.
Я делал это вручную и часто почти сразу получал тождества для всех переменных.

Так вот, сколько я не пробовал , сколько не удалял(в размерностях 4, 5, 6, 9):

• изолировал 1 вершину графа,
• подграф $\mathbf{K}_2\,$ ,
• $\mathbf{K}_3\ (n=9),$ ,
• две вершины оддельно($n=9$),

— Всегда у вектора $v$ получалось 2 разных значения координат! Почему? И это главный вопрос. Может удасться доказать? Но тут я сдаюсь.
При чём, это зависит, где рёбра обнуляються. Если не вру, изолируя третюю кограницу примера выше($n=6$), вектор $v$ получиться тривиальным(все координаты равны).

Сначала я думал, что размерность маленькая, и может быть, есть какая-то большая размерность, в которой можно найти примеры "тернарных" векторов с кограницами разных знаков.. но это наверняка неверно.
Моя лучшая идея - это из-за природы самого отображения. Смутно помню, но оно относиться к первым когомологиям, значит в некотором ко-комплексе оно находиться между ко-цепей порядка 2 и 0.

Может быть, такие случаи ограничены рангом чьих-то гомологий или ко-гомологий? На пример, разности между тремя переменными порождают группу ранга 2, а (ко)гомологии ранга 1, значит такого быть не может.
Но это фигня, ибо при подстановке значений, разности переменных могут совпасть.
Почему я не нашел даже таких примеров — загадка.

А если всё проще? а я Упорно не вижу, почему кограничный образ орбиты вектора может быть ориентирован в разные стороны только, когда у этого вектора 2 разных значения координат.

В заключение, вот примеры таких векторов($x>y$ или $y>x$):
$(x, y, y)$
$(x, y, y, x, y)$
$(x, x, y, x, x)$
$(x, y, x, x, y, x)$
$(x, x, x, y, x, x)$
$(x, x, x, y, x, y)$
$(x, y, x, y, x, y, y, x, y)$