Доброго всем времени суток!
Задали вот такую задачу:
Пусть

- область, а

- голоморфная, неконстантная в
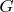
функция. Докажите, что

не достигает своего максимума на
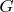
.
Понятно, что задача на принцип максимума модуля. Попробовал несколько подходов: Рассмотрев

и

можно легко показать, что

и

не достигают своего максимума в
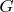
. Отсюда, конечно же, следует, что любая гармоническая (двумерная) функция будет тоже удовлетворять принципу максимума. Проверил для

- в общем случае она не гармоническая. Затем попробовал как-то получить противоречие из того, что

принимает этот максимум (из положительной полуопределенности гессиана) - тоже не вышло. Как-то по-умному выразить

через

тоже не выходит, да и не думаю, что задача на это.