Уважаемы форумчане, столкнулся с такой проблемой. Иногда по структурной схеме нужно определить передаточную функцию, используя стандартные преобразования. Пусть, для примера, имеется такая незаурядная структурная схема.
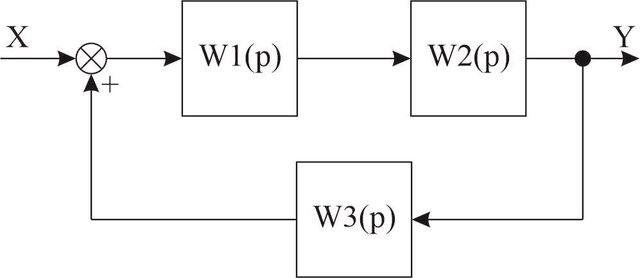
Пусть для примера будут вот такие передаточные функции в звеньях.



Очевидно, что итоговая передаточная функция такой структурной схемы будет иметь вид.

Так вот вопрос. Можно ли про помощи пакета Maxima найти передаточную функцию. В чем проблема, как известно, при выполнении преобразований p сокращать нельзя, из-за этого понижается порядок дифференциального уравнения, стандартная упрощалка Maxima та же самая ratsimp прекрасно сократит p и выражение будет неверным. То же эффект даст и collect из MathCad. Вопрос, может как-то можно Максиме запретить сокращать p, может есть какая-то директива или типа того, подскажите, если не трудно
