Кривошип

, соединяющий оси

и

двух находящихся в зацеплении зубчатых колёс I и II, вращается вокруг неподвижной оси

с постоянной утловой скоростью

. Колесо II вращается в противоположном направлении вокруг оси

с такой же по величине угловой скоростью

. Найти скорость и ускорение точки

обода колеса I в тот момент вре мени, когда

, если ралиус колеса II в три раза больше радиуса колеса I

.
Моё решение:(1) Свяжем ПСО с колесом ||
(2) Условие равенства скоростей в точке зацепления

:
 В этом уравнении для векторов не должно быть минусов, да?
В этом уравнении для векторов не должно быть минусов, да?Перепишем, как:
![$$
[\bar{\omega}_I, \overrightarrow{A F}]+[\bar{\omega}, \overrightarrow{O F}]=0
$$ $$
[\bar{\omega}_I, \overrightarrow{A F}]+[\bar{\omega}, \overrightarrow{O F}]=0
$$](https://dxdy-01.korotkov.co.uk/f/8/0/e/80e9ca5081193c66c63251519545ffba82.png)
(3) Пусть ось

проходит вдоль

, ось

- перпендикулярно

и через точку
 Сейчас допишу остальные пункты...
Сейчас допишу остальные пункты...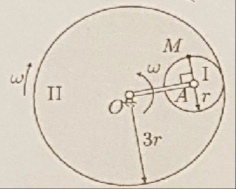 -- 31.10.2024, 17:18 --
-- 31.10.2024, 17:18 --Первое слагаемое (векторное произведение) равно

Второе =

Отсюда:

(4)
![$$
\begin{aligned}
& \overline{V_M}{ }^{\text {отн }}=\overline{V_I}+\left[\overline{\omega_I} \cdot \overline{F M}\right]=\\
& \left.=(3 r \omega) \overline{e_y}+\bar{e}_x(-3 r \omega)+\overline{e_y}(-3 r \omega\right) \\
& =(-3 r \omega) \bar{e}_x
\end{aligned}
$$ $$
\begin{aligned}
& \overline{V_M}{ }^{\text {отн }}=\overline{V_I}+\left[\overline{\omega_I} \cdot \overline{F M}\right]=\\
& \left.=(3 r \omega) \overline{e_y}+\bar{e}_x(-3 r \omega)+\overline{e_y}(-3 r \omega\right) \\
& =(-3 r \omega) \bar{e}_x
\end{aligned}
$$](https://dxdy-03.korotkov.co.uk/f/a/a/2/aa2c8308f3f0bf6c7320cb60d402f73682.png)
Так как
 Как здесь аргументировать, что я нашла относительную скорость?-- 31.10.2024, 17:34 --
Как здесь аргументировать, что я нашла относительную скорость?-- 31.10.2024, 17:34 --(5) Переносной скоростью называется абсолютная скорость той точки ПСК, в которой в данный момент находится точка

:
![$\overline{V_{\text {пер}}}=\overline{V_o}+[\bar{\omega}, \overrightarrow{O M}]=\overline{e_x}(-r \omega)+\overline{e_y}(2 \omega r)$ $\overline{V_{\text {пер}}}=\overline{V_o}+[\bar{\omega}, \overrightarrow{O M}]=\overline{e_x}(-r \omega)+\overline{e_y}(2 \omega r)$](https://dxdy-03.korotkov.co.uk/f/6/7/1/6716b4a697b7a55a0aec313acc930d5e82.png)
(6)
По теореме сложения скоростей

 -- 31.10.2024, 17:45 --
-- 31.10.2024, 17:45 --(7) По формуле Ривальса для тела I, точек AM
![$$
\begin{aligned}
& \bar{a}_M=\bar{e}_x(-4 r \varepsilon)+\bar{e}_y(2 r \varepsilon)= \\
& =\bar{a}_A+[\bar{\varepsilon}, \overline{A M}]+\left[\bar{\varepsilon} \left[\bar{\varepsilon} , \overline{A M}\right]\right]= \\
& =\overline{e_x}(-r \varepsilon)+\overline{e_y}\left(-9 \omega^2 r\right) \end{aligned}
$$ $$
\begin{aligned}
& \bar{a}_M=\bar{e}_x(-4 r \varepsilon)+\bar{e}_y(2 r \varepsilon)= \\
& =\bar{a}_A+[\bar{\varepsilon}, \overline{A M}]+\left[\bar{\varepsilon} \left[\bar{\varepsilon} , \overline{A M}\right]\right]= \\
& =\overline{e_x}(-r \varepsilon)+\overline{e_y}\left(-9 \omega^2 r\right) \end{aligned}
$$](https://dxdy-03.korotkov.co.uk/f/2/5/0/2504392f1e09f4688a27faee9c3e89ad82.png)
Правда же, что

?
Вот на это шаге, если приравнять коэффициенты при каждой координате, получается противоречие...
Где ошиблась?