У нас это была задача со звездочкой на третьем курсе. Хорошего решения я не знаю.
Плохое - заметить, что у нас есть последовательность функций единичной нормы, такая что

-я функция равна нулю во всех точках

. Считаем, что последовательность точек, на которых достигается норма, сходится к какой-то точке

, и строим последовательность

, быстро сходящуюся к

, такую что

велико. И дальше написав

с подходящими коэффициентами (не слишком быстро и не слишком медленно убывающими) получить что

не существует - выбором знаков можно добиться, чтобы первые

слагаемых были положительны, выбором соотношения
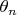
и

можно добиться, чтобы слагемые после

-го не очень влияли.
(если надо, у меня есть полное решение, даже в

, оно не особо интересное)
Следовательно эти нормы на

эквивалентны
А что в этом плохого?
Верно ли, что замкнутое подпространство

, целиком лежащее в

, конечномерно?
В

слабая и сильная сходимость эквивалентны, а любое замкнутое подпространство

либо конечномерно, либо гильбертово.
Попробовал обобщить: если

-- всюду плотное подпространство в банаховом пространстве

, то замкнутое подпространство

, целиком лежащее в

, конечномерно
Пусть

- Ваше любимое банахово пространство,

- его всюду плотное незамкнутое подпространство. Возьмем

,

,

.