Рекурсия для H(t,x,z) из A140717

[kthxbye]

Имеется последовательность A140717 (треугольник читаемый построчно). Там приведена производящая функция

$$G(t,z) = H(t,\frac{1}{t},z)$$

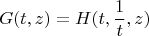
где

$$H(t,x,z) = 1 + zH(t,x,z)(H(t,tx,z)-1+tx)$$

Я обнаружил относительно быстрый алгоритм для вычисления строк треугольника рекурсивно. Вот пример его работы на PARI/GP:

upto1(n) = my(v1); v1 = vector(n, i, 1); v2 = vector(n, i, 0); v2[1] = 1; for(i=1, n-1, for(j=i+1, n, A = v1[i]; B = v1[j]; v1[i] = A + z^(j-i)*B; v1[j] = z*A + B); v2[i+1] = v1[i+1]); v2
pr1(n) = my(v1); v1 = upto1(n); for(i=1, n, print(Vecrev(v1[i])))
pr1(20)

Хочется, как минимум, сверить результаты, однако я не понимаю, как задавать $H(t,x,z)$.

Вопрос: как правильно рекурсивно задается $H(t,x,z)$?