Пусть

это произвольная функция с целочисленными значениями.
Пусть

это целочисленная последовательность с производящей функцией

, где

это цепная дробь, такая, что

Заметьте, что

Пусть

это целочисленная последовательность, такая, что

Пусть
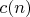
это то же, что и

(после полной трансформации), где мы начинаем с массива

длины

с элементами

. Для

от

до

и (внутри) для

от

до

(т.е. это два вложенных цикла) будем последовательно применять
![$[\nu_i, \nu_j] = [\nu_i + f(j-i)\nu_j, \nu_i + f(j-i)\nu_j]$ $[\nu_i, \nu_j] = [\nu_i + f(j-i)\nu_j, \nu_i + f(j-i)\nu_j]$](https://dxdy-03.korotkov.co.uk/f/a/9/b/a9b80e576ee0276146ecd9d67f77f51082.png)
.
После множества численных экспериментов я заметил, что для абсолютно любой

выполняется следующее:

.
Вот код на PARI/GP для проверки:
Код:
f(n) = n
c(n) = my(v1); v1 = vector(n, i, 1); for(i=1, n-1, for(j=i+1, n, A = v1[i] + f(j-i)*v1[j]; v1[i] = A; v1[j] = A)); v1[n]
upto1(n) = my(v1); v1 = vector(n, i, c(i))
h(n,x) = my(CF = 1); for(i=1, n, CF = 1 - f(n - i + 1)*x/CF + x*O(x^n)); 1/CF
upto2(n) = my(v1); v1 = Vec(h(n,x)); v2 = vector(n+1, i, 0); v2[1] = 1; for(i=1, n, v2[i+1] = sum(j=0, i-1, v2[j+1]*v1[i-j])); v2 = vector(n, i, v2[i+1])
test(n) = upto1(n) == upto2(n)
Существует ли способ как-нибудь доказать это?