Можно ли считать условия и формулы верными? 1) Длина дуги кривой в декартовых координатах, когда функция

задана явно

Условия:
- Функция

непрерывна и дифференцируема на интервале
![$[a, b]$ $[a, b]$](https://dxdy-04.korotkov.co.uk/f/b/d/4/bd4455e79810acc06e3d31c60fb8bfb282.png)
.
2) Длина дуги кривой в декартовых координатах, когда функция задана параметрически

Условия:
- Параметрические функции
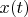
и
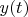
непрерывны и дифференцируемы на интервале
![$[t_1, t_2]$ $[t_1, t_2]$](https://dxdy-01.korotkov.co.uk/f/4/f/d/4fd7e1029c498a5313f07c76d75fcbb382.png)
.
3) Длина дуги кривой в полярной системе координат, ограниченная двумя кривыми
Формула:

Условия:
- Полярная функция

непрерывна и дифференцируема на интервале
![$[\theta_1, \theta_2]$ $[\theta_1, \theta_2]$](https://dxdy-04.korotkov.co.uk/f/3/e/5/3e5f3be970be5b8018309a7f3fb93c9982.png)
.
4) Объем тела вращения вокруг оси

Формула:
![$ V = \pi \displaystyle\int_{a}^{b} \left[ f(x) \right]^2 \, dx $ $ V = \pi \displaystyle\int_{a}^{b} \left[ f(x) \right]^2 \, dx $](https://dxdy-01.korotkov.co.uk/f/0/0/3/0036faf14dcf763df251840d2c95e23982.png)
Условия:
- Функция

непрерывна на интервале
![$[a, b]$ $[a, b]$](https://dxdy-04.korotkov.co.uk/f/b/d/4/bd4455e79810acc06e3d31c60fb8bfb282.png)
.
5) Объем тела вращения вокруг оси

Формула:
![$ V = \pi \displaystyle\int_{c}^{d} \left[ g(y) \right]^2 \, dy $ $ V = \pi \displaystyle\int_{c}^{d} \left[ g(y) \right]^2 \, dy $](https://dxdy-02.korotkov.co.uk/f/1/c/5/1c5a8107a90f860ab9a32847401c782a82.png)
Условия:
- Функция

непрерывна на интервале
![$[c, d]$ $[c, d]$](https://dxdy-01.korotkov.co.uk/f/c/4/b/c4b64e13e803ece9342b976287f5265e82.png)
.
6) Площадь поверхности тела вращения вокруг оси

Формула:

Условия:
- Функция

непрерывна и дифференцируема на интервале
![$[a, b]$ $[a, b]$](https://dxdy-04.korotkov.co.uk/f/b/d/4/bd4455e79810acc06e3d31c60fb8bfb282.png)
.
7) Площадь поверхности тела вращения вокруг оси

Формула:

Условия:
- Функция

непрерывна и дифференцируема на интервале
![$[c, d]$ $[c, d]$](https://dxdy-01.korotkov.co.uk/f/c/4/b/c4b64e13e803ece9342b976287f5265e82.png)
.
-- 08.08.2024, 19:31 --Вроде бы есть какие-то шансы использовать не обратные функции в пунктах 5 и 7, если не ошибаюсь. Если да, то как именно должны выглядеть условия?