Исправленная версия для трех точек. Оказалась не такой простой, также возможны ошибки!
Но Geogebra вроде верифицирует точку

как центроид.
При радиусе окружности

строим вспомогательную окружность с центром в

на луче
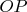
и радиусом

. Точка

свободно перемещается по окружности, а точка

Далее два случая:
1. Построенная малая окружность целиком лежит внутри основной.
Тогда при произвольном положении

на окружности точка

будет лежать внутри нее,
и если построить

на окружности так, что

, точка

будет центроидом
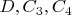

2. Малая окружность пересекает основную в точках

.
При этом линии

и

пересекают основную окружность в

.
Тогда искомое построение будет верным, если

лежит на дуге

.
 -- 30.07.2024, 23:09 --
-- 30.07.2024, 23:09 --Для четного числа требуемых точек

есть такая идея.
Внутри окружности строим

точек так, что

будет их центром масс.
Самое красивое - правильный

-угольник.
Для каждой вершины строим пару "проекций" на окружность так, что вершина - их центр масс.
Тогда

будет ц.м. этих проекций.
Далее два вопроса, с учетом того, что

-угольник может меняться как минимум
по двум параметрам - размеру стороны и углу поворота.
1. Детский вопрос. Доказать, что существует такой

-угольник, что

полученных проекций
все будут различны.
2. Взрослый вопрос. Найти такую конфигурацию, чтобы

точек на окружности были максимально рассеяны
(максимум минимального углового расстояния) и при этом

была их ц.м.
Если на эти вопросы сложно ответить для многоугольника, можно попробовать другие конфигурации
точек, для которых

ц.м., например лежащие на одной линии.
Для меня это все сложновато, но интересно )