Это стандартный вопрос, просто мне интересно посмотреть, как эти вещи выводятся в лоб, из общих фактов об уравнении уравнения Гамильтона-Якоби они выводятся мгновенно.
Дело происходит на римановом многообразии

с локальными координатами

и метрикой

.
Пусть

-- геодезическая, и

-- натуральный параметр.
Пусть функция

является решением уравнения

Доказать, что если геодезическая

начинается на поверхности уровня
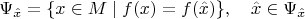
и перпендикулярна ей то
1) она перпендикулярна каждой поверхности уровня

, которую пересекает;
2)
