Используйте критерий Коши равномерной сходимости интеграла.
VavilenИнтеграл расходится при

, поэтому в этом случае можно записать отрицание критерия Коши. Далее, если воспользоваться непрерывностью по параметру интеграла по промежутку, отделённому от единицы, получается отрицание критерия Коши равномерной сходимости.
Проделал такие выкладки - отрицание критерия Коши:

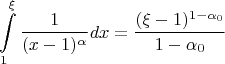
Тогда если взять

То есть нет равномерной сходимости на

? Правильно понимаю, что при этом на
![$[-1;\frac{1}{2}]$ $[-1;\frac{1}{2}]$](https://dxdy-02.korotkov.co.uk/f/9/c/0/9c01894d602461f4d82402e9e22a15c282.png)
например интеграл сходится равномерно?