Однажды возникла передо мною следующая задача.
В некотором не менее чем трёхмерном евклидовом пространстве

заданы три вектора:

и

.
Также известно, что


Требуется построить из

такие три линейные комбинации

и
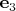
, чтобы выполнялись условия

Я эту задачу тут же решил, не прибегая к стандартным методам и опираясь лишь на так называемую "наглядно-геометрическую интуицию". А потом призадумался, насколько очевидно это решение?
Попробуйте повторить, интересно, что выйдет.
(ОТВЕТ)