daogiauvang писал(а):
Дан функция непрерывна на

причем

.
Доказать, что

По определению

.
Если

, то

откуда

и

- значит непрерывная функция

строго монотонна.
Если

для некоторого

, то в силу строгой монотонности

либо для

, либо для

- что противоречит неотрицательности функции:

. Значит

при

.
Если

строго убывает, то

при

, в том числе

, но для

должно быть

. Противоречие. Значит

строго возрастает.
Если

, то

при

, в том числе

, но должно быть

. Значит

и
![$f[[0,+\infty)]=[0,+\infty)$ $f[[0,+\infty)]=[0,+\infty)$](https://dxdy-04.korotkov.co.uk/f/3/4/1/341648f087ca086a463a8fb363e8e30382.png)
, а

имеет обратную на

.
Если

, то

при

, в том числе

, а если

, то

при
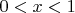
, в том числе

, но должно быть

. Значит

.
Пусть

,

,

- дизъюнктное разбиение

, то есть

,

,

- не пересекаются, и

.
Если

, то

и

, что означает

.
Если

, то

и

, что означает

.
Если

, то

и

, что означает

.
Множества

,

и

биективно-инвариантны относительно преобразований

и

.
Отсюда следует, в частности, учитывая непрерывность

, что на любом интервале

при

и на любом интервале

при
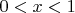
существует

.
Возмем некоторое

(то есть

), что

.
Определив

и

для натуральных

, будем иметь:

,

(

),

,

и
![$f[[x_n,x_{n+1}]]=[x_{n-1},x_n]$ $f[[x_n,x_{n+1}]]=[x_{n-1},x_n]$](https://dxdy-02.korotkov.co.uk/f/5/f/7/5f76b54da1d1b4764d87e58ec02ebaaf82.png)
.
Для любой непрерывной строго возрастающей функции
![$g:[x_0,x_1]\to[x_{-1},x_0]$ $g:[x_0,x_1]\to[x_{-1},x_0]$](https://dxdy-01.korotkov.co.uk/f/c/2/6/c266c792c344cf5f4687e0918a6b4f6282.png)
, такой что

и

, существует единственная на интервале
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
функция

с указанными в условии свойствами, такая, что на интервале
![$[x_0,x_1]$ $[x_0,x_1]$](https://dxdy-02.korotkov.co.uk/f/5/b/4/5b42f280124c8c64933c2b4a6cd9fd7c82.png)
она совпадает с

:
то есть, если
![$g|_{[x_0,x_1]}=f_1|_{[x_0,x_1]}$ $g|_{[x_0,x_1]}=f_1|_{[x_0,x_1]}$](https://dxdy-04.korotkov.co.uk/f/3/4/9/349cb80b24a8fb4dba5d5052e0dd9d4382.png)
и
![$g|_{[x_0,x_1]}=f_2|_{[x_0,x_1]}$ $g|_{[x_0,x_1]}=f_2|_{[x_0,x_1]}$](https://dxdy-04.korotkov.co.uk/f/3/2/4/32447ab1ae2b8d1ea074fe8285bc15fb82.png)
, то
![$f_1|_{[0,1]}=f_2|_{[0,1]}$ $f_1|_{[0,1]}=f_2|_{[0,1]}$](https://dxdy-01.korotkov.co.uk/f/0/d/3/0d32a5294dcb7890830b141319ab3a7f82.png)
.
Эта единственная на интервале
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
функция

задается на нем
- при
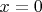
, как

;
- при
![$x\in[x_{2n-1},x_{2n}]$ $x\in[x_{2n-1},x_{2n}]$](https://dxdy-01.korotkov.co.uk/f/c/7/f/c7fb7d39cc5bc1f5d0b35ae98260ef1882.png)
, что дает
![$f^{(2n)}(x)\in[x_{-1},x_0]$ $f^{(2n)}(x)\in[x_{-1},x_0]$](https://dxdy-01.korotkov.co.uk/f/8/f/3/8f3578d39bd509b8dea4f7bf6fbf74af82.png)
, как

![$=f^{(-2n+2)}(g^{(-1)}(f^{(2n)}(x)))=(g^{(-1)}(x^{2^n}))^{2^{-(n-1)}}\in[x_{2n-2},x_{2n-1}]$ $=f^{(-2n+2)}(g^{(-1)}(f^{(2n)}(x)))=(g^{(-1)}(x^{2^n}))^{2^{-(n-1)}}\in[x_{2n-2},x_{2n-1}]$](https://dxdy-01.korotkov.co.uk/f/8/0/5/805195d6048cc09b5e6156735091a15b82.png)
;
- при
![$x\in[x_{2n},x_{2n+1}]$ $x\in[x_{2n},x_{2n+1}]$](https://dxdy-04.korotkov.co.uk/f/f/0/c/f0c7c7697c36f5df39c0c6c5b097ea2e82.png)
, что дает
![$f^{(2n)}(x)\in[x_0,x_1]$ $f^{(2n)}(x)\in[x_0,x_1]$](https://dxdy-04.korotkov.co.uk/f/7/7/1/7712a032a60892fc3505e0ebb2a26f2f82.png)
, как
![$f(x)=f^{(-2n)}(f(f^{(2n)}(x)))=f^{(-2n)}(g(f^{(2n)}(x)))=(g(x^{2^n}))^{2^{-n}}\in[x_{2n-1},x_{2n}]$ $f(x)=f^{(-2n)}(f(f^{(2n)}(x)))=f^{(-2n)}(g(f^{(2n)}(x)))=(g(x^{2^n}))^{2^{-n}}\in[x_{2n-1},x_{2n}]$](https://dxdy-03.korotkov.co.uk/f/2/d/a/2da30172ccfbc93c9a08dcd577060b3682.png)
;
- при

, как

;
то есть:
![$f(x)|_{[0,1]}=\left\{\begin{array}{cccc}0, & x=0\\(g^{(-1)}(x^{2^n}))^{2^{-(n-1)}}, & x\in[x_{2n-1},x_{2n})\wedge n\in\mathbb{Z}\\(g(x^{2^n}))^{2^{-n}}, & x\in[x_{2n},x_{2n+1})\wedge n\in\mathbb{Z}\\1, & x=1\end{array} \right$ $f(x)|_{[0,1]}=\left\{\begin{array}{cccc}0, & x=0\\(g^{(-1)}(x^{2^n}))^{2^{-(n-1)}}, & x\in[x_{2n-1},x_{2n})\wedge n\in\mathbb{Z}\\(g(x^{2^n}))^{2^{-n}}, & x\in[x_{2n},x_{2n+1})\wedge n\in\mathbb{Z}\\1, & x=1\end{array} \right$](https://dxdy-04.korotkov.co.uk/f/3/5/c/35c137e587688a14fb394800a1e95ed382.png)
Тогда

Учитывая, что

при

и

при

получим:



Функция

, заданная на интервале

, инвариантна относительно преобразований

и

. поэтому можно рассмотреть ее значения на интервале одного периода
![$[(\frac{1}{2})^{\sqrt[4]{2}},(\frac{1}{2})^{\frac{1}{\sqrt[4]{2}}}]=[0.4385438119798300.., 0.5582965649524321..]$ $[(\frac{1}{2})^{\sqrt[4]{2}},(\frac{1}{2})^{\frac{1}{\sqrt[4]{2}}}]=[0.4385438119798300.., 0.5582965649524321..]$](https://dxdy-03.korotkov.co.uk/f/a/3/c/a3cf05ae0afeb08197522d7b4a97c07c82.png)
.
Дальнейший анализ - только численно.
Удивительно, но эта функция
почти констата!

![$A_-((\frac{1}{2})^{\sqrt[4]{2}})=A_-((\frac{1}{2})^{\frac{1}{\sqrt[4]{2}}})=0.22964740110\textbf{337883997551757390..}$ $A_-((\frac{1}{2})^{\sqrt[4]{2}})=A_-((\frac{1}{2})^{\frac{1}{\sqrt[4]{2}}})=0.22964740110\textbf{337883997551757390..}$](https://dxdy-04.korotkov.co.uk/f/3/1/8/318bc60424061106b5ce01f457c2f71a82.png)
График


Минимум

есть при

и равен

.
Это меньше, чем

.
Для

же интеграл будет

- явно где-то среднее между максимумом и минимумом интеграла, взятых по всем функциям

.
Значит такого анализа недостаточно. Когда мы подставляли минимумы

и

, мы не учли зависимости между

и

, и что когда

- стремится к своему допустимому минимуму, то

- стремится к своему допустимому максимуму. Это увеличит оценку снизу.
Дальнейший анализ.
Переходя к переменной

,

,

,
![$t\in[x_{-1},x_0]$ $t\in[x_{-1},x_0]$](https://dxdy-02.korotkov.co.uk/f/1/3/9/139d9bdac776980b1ca57bd2606e732482.png)
при
![$x\in[x_{2n-1},x_{2n}]$ $x\in[x_{2n-1},x_{2n}]$](https://dxdy-01.korotkov.co.uk/f/c/7/f/c7fb7d39cc5bc1f5d0b35ae98260ef1882.png)
и
![$t\in[x_0,x_1]$ $t\in[x_0,x_1]$](https://dxdy-01.korotkov.co.uk/f/c/c/4/cc4ba3726bc075f5e810b8aa9c2f442482.png)
при
![$x\in[x_{2n},x_{2n+1}]$ $x\in[x_{2n},x_{2n+1}]$](https://dxdy-04.korotkov.co.uk/f/f/0/c/f0c7c7697c36f5df39c0c6c5b097ea2e82.png)
, получим:

Что дальше?..