Цепи Маркова.Разложение на классы

[Stensen]

Всем доброго времени суток. Уважаемые, помогите разобраться. Есть граф и матрица вероятностей переходов:



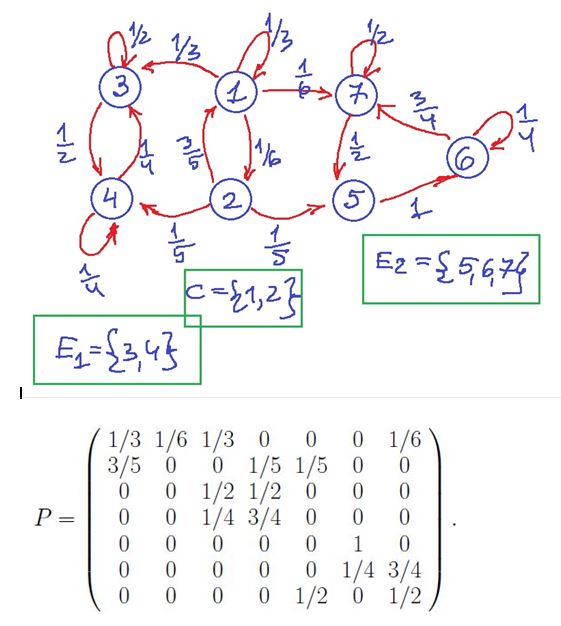
Определены замкнутые классы существенных состояний: $E_1=\left\lbrace 3,4 \right\rbrace, E_2=\left\lbrace 5,6,7 \right\rbrace$ и несущественные состояния $C=\left\lbrace 1,2 \right\rbrace$ , (матрица распадается на квадратики).

1.Найдены финальные вероятности внутри замкнутых классов $E_1: \left\lbrace \pi_3=\frac{1}{3}, \pi_4=\frac{2}{3} \right\rbrace, E_2 : \left\lbrace \pi_5=\frac{3}{13}, \pi_6=\frac{4}{13}, \pi_7=\frac{6}{13} \right\rbrace$

2.Найдены вероятности перехода из существенного состояния в замкнутые классы $E_1, E_2$, состоящие из этих же состояний:

в $ E_1 : p_3_{E_1}=p_4_{E_1}=1$,

в $E_2 : p_5_{E_2}=p_6_{E_2}=p_7_{E_2}=1 $

Вопрос1: Правильно я понимаю, что вероятности перехода из существенного состояния в замкнутый класс, состоящий из этих же состояний, всегда равны 1?

3.Найдены вероятности перехода из несущественных состояний в замкнутые классы $E_1, E_2$ из уравнений: $p_i_{S_k}=\sum\limits_{j \in T} p_i_j p_j_{S_k} + \sum\limits_{j\in S_k} p_i_j$ , где: $T, S_k$ - множества несущественных и существенных состояний, соответственно.

$p_1_{E_1}= \frac{1}{3} + \frac{1}{3} p_1_{E_1} + \frac{1}{6} p_2_{E_1} \to p_1_{E_1}= \frac{11}{17}$

$p_2_{E_1}= \frac{1}{5} + \frac{3}{5} p_1_{E_1} \to p_2_{E_1}= \frac{10}{17}$


далее у автора:

$p_1_{E_2}= 1- p_1_{E_1} = \frac{6}{17}$

$p_2_{E_2}= 1- p_2_{E_1} = \frac{7}{17}$

Вопрос2: $p_1_{E_2}, p_2_{E_2} я мог бы найти по тому же уравнению. У автора проще. Правильно я понимаю, что для замкнутых классов должны выполняться условия нормировки: $ $$\sum\limits_{k}$$p_i_{E_k}=1 ?

4.Для начального распределения $p(0)= \left\lbrace 1,0,0,0,0,0,0\right\rbrace $ автором получено финальное распределение :

$ \pi = \left\lbrace 0,0, \frac{11}{17} \cdot \frac{1}{3}, \frac{11}{17} \cdot \frac{2}{3} , \frac{6}{17} \cdot \frac{3}{13}, \frac{6}{17} \cdot \frac{4}{13} , \frac{6}{17} \cdot \frac{6}{13} \right\rbrace $

Вопрос3: не смог понять, как вычислено это финальное распределение для заданного начального? Поясните пожалуйста.

Вопрос4: посоветуйте литературу "задачи с решениями" на нахождение распределений в приводимых цепях

[Stensen]

Всем доброго времени суток.

Stensen в сообщении #1641469 писал(а):

Для начального распределения $p(0)= \left\lbrace 1,0,0,0,0,0,0\right\rbrace $ получено финальное распределение :

$ \pi = \left\lbrace 0,0, \frac{11}{17} \cdot \frac{1}{3}, \frac{11}{17} \cdot \frac{2}{3} , \frac{6}{17} \cdot \frac{3}{13}, \frac{6}{17} \cdot \frac{4}{13} , \frac{6}{17} \cdot \frac{6}{13} \right\rbrace $

не смог понять, как вычислено это финальное распределение для заданного начального?

Вроде разобрался. Поправьте пожалуйста, если не прав. Вероятности нахождения в несущественных $1,2$ состояниях (нулевых) равны нулю. Остался вопрос:

Правильно я понимаю, начиная в замкнутых классах $E_1, E_2$ с начальным распределением любым из: $(0,0,1,0,0,0,0), (0,0,0,1,0,0,0), (0,0,0,0,1,0,0), (0,0,0,0,0,1,0), (0,0,0,0,0,0,1)$, то там и останемся: : $\lim\limits_{n\to\infty}p_{ij}=p_j $ с финальным распределением:

в $E_1$: $(0,0,\pi_3,\pi_4,0,0,0)$

в $E_2$: $(0,0,0,0,0,0,\pi_5,\pi_6,\pi_7)$, т.к. финальная вероятность состояния неразложимой апериодической подцепи не зависит от начального состояния, где:

$(\pi_3,\pi_4)$ и $(\pi_5,\pi_6,\pi_7)$ стационарные распределения в классах $E_1,\, E_2$ соответственно.

Найдем финальное распределение $\pi =(P_1, P_2, P_3, P_4, P_5, P_6, P_7)$.

Т.к. $1,2$ это невозвратные и нулевые состояния, то $P_1=P_2=0$ .

При начальном $\pi(0)=(1,0,0,0,0,0,0)$ , выходя из состояния $1$:

$P_3=p_1(0) \cdot p_{1E_1} \cdot \pi_3$

$P_4=p_1(0) \cdot p_{1E_1} \cdot \pi_4$

$P_5=p_1(0) \cdot p_{1E_2} \cdot \pi_5$

$P_6=p_1(0) \cdot p_{1E_2} \cdot \pi_6$

$P_7=p_1(0) \cdot p_{1E_2} \cdot \pi_7$

При начальном $\pi(0)=(0,1,0,0,0,0,0)$, выходя из состояния $2$:

$P_3=p_2(0) \cdot p_{2E_1} \cdot \pi_3 $

$P_4=p_2(0) \cdot p_{2E_1} \cdot \pi_4$

$P_5=p_2(0) \cdot p_{2E_2} \cdot \pi_5$

$P_6=p_2(0) \cdot p_{2E_2} \cdot \pi_6$

$P_7=p_2(0) \cdot p_{2E_2} \cdot \pi_7$ ,

где: $p_1(0), \, p_2(0)$ вероятности нахождения в состояниях 1,2 соответственно в начальный момент.