Аппроксимация распределения

[denny]

Занимаюсь непериодическими двоичными последовательностями типа Thue-Morse.
Научился находить подстановки, которые порождают интересные, "богатые" на всякие свойства последовательности.
Заинтересовался распределением пар, троек и т.д. в них.
Например, в Thue-Morse $0$ и $1$ встречаются равновероятно,
пары $01$ и $10$ - в два раза чаще, чем $00$ и $11$.
А из восьми троек вообще встречаются только четыре.

Правило $11 \to 00, 00 \to 01, 0 \to 10$ порождает гораздо более богатую в этом смысле последовательность.
Вот графики относительных количеств пар, троек и т.д. вплоть до сочетаний из 10 битов
в порождаемой эти правилом последовательности
(в Log-Log осях):

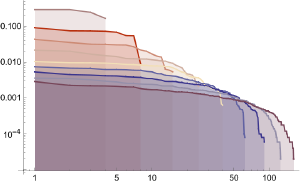
Что это может быть за распределение?? Я пытался аппроксимировать power law, broken power law,
power law with exp cut-off и т.д., все не то...

[ozheredov]

denny в сообщении #1638970 писал(а):

broken power law

Да, первые три сверху чрезвычайно похожи на BPL, причем у каждого следующего распределения число точек перелома увеличивается. Интересно ) Последующие скорее всего тоже BPL, просто число changePoint'ов становится катастрофически большим.