Привет участникам форума!
Нашел интересный и не очень понятный случай в одной книге.
Автор выводит выражение для модуля суммы двух векторов.
Складывает два вектора, получает треугольник и далее через теорему косинусов приходит к выражению:

если вектора a и b прямопротивоположные и угол между ними составляет

, то у автора получается:
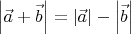
.
Но модуль вектора b может оказаться больше модуля вектора a, так что модуль суммы получится отрицательным? Автор ошибся? Может, надо было и справа модуль взять?