Квазиклассическое приближение, с необходимыми оценками точности и с условиями применимости, - сложная тема. Соответственно, и аккуратный вывод "правил Бора-Зоммерфельда" не является простым. В большинстве учебников, где говорится о ВКБ-приближении, вывод есть. Пытаться подменять серьёзный вывод каким-то упрощённым своим велосипедом - плохая идея.
"Приближения" (14), (15) не обоснованы оценками. По этим формулам коэффициенты на разных участках различаются только фазовыми множителями. Вряд ли это верно.
На мой взгляд, лучше оставить в покое "правила Бора-Зоммерфельда" и просто со ступенчатым потенциалом типа (1) порешать разные задачи; среди них есть много поучительных.
Только надо уточнить формулировки. Например, из формул (5), в которых

видно, что

нумерует границы участков. Поскольку крайняя правая граничная точка

имеет номер

то область

имеет номер

Область

имеет номер ноль. Коэффициенты нумеруются так же, как участки. Значит, в стационарных состояниях, локализованных в яме (т.е с энергией

меньшей высоты стенок ямы) должно быть

и

Суммирование в (3) будет до

причём,

есть произвольное значение, оно влияет только на выбор фазы для

Равенства

и

неверные. Чётность или нечётность связывает друг с другом значения волновой функции на разных участках - расположенных симметрично относительно центра ямы, а не на участке с одним и тем же номером

Задачи со ступенчатыми потенциалами (притом не обязательно с участками одинаковой длины, можно и с разными длинами

удобно решать методом "матриц переноса". Одна из возможных формулировок этого метода вот какая. Вместо

и

рассматриваем

и

Тогда из условий типа (6) и (7) имеем:

где матрица
![$$\hat{t}^{(j)}=\left[\begin{array}{cc}\dfrac{k_j+k_{j+1}}{2\sqrt{k_jk_{j+1}}}e^{-ik_{j+1}l_{j+1}}&\dfrac{k_j-k_{j+1}}{2\sqrt{k_jk_{j+1}}}e^{ik_{j+1}l_{j+1}}\\ \dfrac{k_j-k_{j+1}}{2\sqrt{k_jk_{j+1}}}e^{-ik_{j+1}l_{j+1}}&\dfrac{k_j+k_{j+1}}{2\sqrt{k_jk_{j+1}}}e^{ik_{j+1}l_{j+1}} \end{array}\right]$$ $$\hat{t}^{(j)}=\left[\begin{array}{cc}\dfrac{k_j+k_{j+1}}{2\sqrt{k_jk_{j+1}}}e^{-ik_{j+1}l_{j+1}}&\dfrac{k_j-k_{j+1}}{2\sqrt{k_jk_{j+1}}}e^{ik_{j+1}l_{j+1}}\\ \dfrac{k_j-k_{j+1}}{2\sqrt{k_jk_{j+1}}}e^{-ik_{j+1}l_{j+1}}&\dfrac{k_j+k_{j+1}}{2\sqrt{k_jk_{j+1}}}e^{ik_{j+1}l_{j+1}} \end{array}\right]$$](https://dxdy-02.korotkov.co.uk/f/9/f/2/9f212badcfcfd66c9c49d0f317dac75582.png)
Коэффициенты крайних участков связаны произведением таких матриц:

где

Другими словами, если нумеровать элементы матрицы

номерами

и

то:


Матрицы

а с ними и матрица

являются унимодулярными: их определители равны единице.
Выделяются два типа задач:
В задачах про энергетические уровни в яме (т.е. когда энергия

ниже высоты потенциальных стенок в крайних областях) должно выполняться условие

при

Поэтому

и

Значит:

Отсюда следует, поскольку

что

Это уловие,

есть точное трансцендентное уравнение, которым определяются уровни

в яме со ступенчатым потенциалом. (Если очень хочется, попытайтесь извлечь из него "правила Бора-Зоммерфельда", с обоснованием и оценками; я не знаю, как.)
Пример учебного сюжета типа расчётного задания для студентов: можно начать с ямы с плоским дном, и смотреть, как изменяется спектр уровней, если в середине ямы выращивать барьер, меняя его толщину и/или высоту. Ещё пример: посмотреть, как расщепляются уровни в двух ямах, первоначально разделённых толстым и высоким барьером, при уменьшении его высоты и/или толщины; различаются случаи симметричных и несимметричных ям.
Второй тип задач - вычисление вероятности

прохождения частицы и вероятности отражения

через барьеры/ямы, когда энергия частицы

превышает значения потенциала

и

в крайних областях. Пусть источник частиц имеется только слева от участков ступенчатого потенциального рельефа (при

Тогда

Величина

определяет плотность потока вероятности
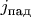
, падающего из источника на потенциальный рельеф слева направо:

Отражённый поток (назад, в область "0") и прошедший вперёд (в область "J+1") соответственно есть:

Вероятности определяются отношениями потоков:


С помощью равенств

искомые вероятности выражаются через элементы матрицы


Интересный учебный сюжет: рассмотреть квазистационарные состояния в яме между двумя барьерами конечной толщины и высоты, рассчитать вероятность

туннелирования через такую пару барьеров, изобразить характерные "пики" на графике зависимости

- эффект резонансного туннелирования.