Коэффициенты в факторизации 0,1-полиномов

[denny]

Пусть $P_{m_2}(x)$ - полином, коэффициенты которого суть цифры двоичного представления числа $m$.
Ранее я заинтересовался корнями $0,1$-полиномов, получилась интересная дискуссия
Но в случае корней не имеет особого значения способ получения полинома;
генерация через двоичные представления просто одна из форм перебора.

Стало интересно, что происходит с факторизацией этих полиномов, а точнее с коэффициентами.
Мне подсказали, что все полиномы-сомножители в факторизации также будут $0,1$-полиномами
"iff there are no carries when multiplying prime factors in binary".
То есть здесь уже прямую роль играет число $m$, из которого получился полином.

Появился наивный вопрос:
Когда в коэффициентах факторизации впервые появится данное целое число $z$?
Первые наблюдения:
$P_{9_2}(x) = 1+x^3 = (1+x)(1-x+x^2)$ - первое появление $z = -1$
$P_{141_2}(x) = 1+x^2+x^3+x^7 = (1+x)(1-x+2x^2-x^3+x^4-x^5+x^6)$ - первое появление $z=2$

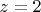
Есть теоретический результат: $1+x^n$ разлагается в круговые полиномы.
А среди коэффициентов круговых полиномов рано или поздно встретится любое целое
(где-то в статье есть пруф)
Поскольку $1+x^n$ - $0,1$-полином, то можно утверждать, что любое целое встретится и в их разложении.
Но это - чистое доказательство существования. Поэтому я продолжил наблюдения.

Выяснилось следующее:
1. Целые числа впервые появляются как коэффициенты в разложении $0,1$-полиномов в порядке
A001057 (если полиномы генерируются из бинарников последовательных натуральных).
Сначала мне показалось, что это очевидно, но в результате, так и не понимаю, почему это так.
2. До $z=-3$ целые появляются строго последовательно. Начиная с $z = 4$ они появляются только попарно,
как ${-z, z}$. Это тем более непонятно.

Проверил ситуацию с $P_{m_3}(x)$, т.е. с $0,1,2$-полиномами. Первое наблюдение сохраняется, более того,
в этом случае они появляются строго последовательно вплоть до $z = 13$, далее еще не проверял.

Если кому-то будет интересна эта тема, буду признателен за любые теоретические результаты и дополнения в численных примерах!

[denny]

Странно, но кроме $0,1$-полиномов я не могу найти даже как называются полиномы,
образованные из чисел заменой основания на $x$.
Провел вычисления для основания $10$. Получается, что целые $z$ появляются
первый раз в следующем порядке:

$$1, 2, 3, 4, 5, 6, 7, 8, 9, 0, -1, -2, -3, -4, -5, -6, -7, -8, 10, 11,$$ $$12, 13, 14, 15, 16, 17, -9, -10, -11, -12, -13,18, -14, -15, -16, -17, $$ $$-18, 19,20, 21, 22, 23, 24, 25, \dots$$

При этом $z=-1$ впервые появляется при $n =1001$ ,$z = 10$ - при $n=28119 $
$z=20$ при $n=60841209$ и т.д.
Неужели в этом нет никакой закономерности?