Цилиндрическая сигма-алгебра

[RikkiTan1]

Доброго времени суток!
Пусть $\mathcal{B}(\mathbb{R}^{[0,1]})$ цилиндрическая сигма-алгебра на $\mathbb{R}^{[0,1]}$, т.е. сигма-алгебра, порожденная всевозможными множествами вида

$$ C=\{x=x(t):(x_{t_1},\ldots,x_{t_n})\in B\in\mathcal{B}(\mathbb{R}^n)\}, $$

где $t_j\in[0,1].$
Известно, что для каждого $A\in\mathcal{B}(\mathbb{R}^{[0,1]})$ существует такая последовательность $\{t_j\}\in[0,1]$ и такое множество $B\in\mathcal{B}(\mathbb{R}^\infty)$, что $A=\{x=x(t):(x_{t_1},\ldots, x_{t_n},\ldots)\in B\}$.
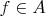
Пусть $A\in\mathcal{B}(\mathbb{R}^{[0,1]})$ не пусто и $A=\{x=x(t):(x_{t_1},\ldots, x_{t_n},\ldots)\in B\}$. Пусть $f\in A$ ($A$ не пусто). Поскольку ограничения на $f$ наложены только для точек $t_j$, то множеству $A$ будут принадлежать все функции, совпадающие с $f$ в этих точках. Таких функций в точности $2^c$. Получается, что каждое непустое множество из $\mathcal{B}(\mathbb{R}^{[0,1]})$ имеет мощность $2^c$. Отсюда заключаем, что, например, множество всех непрерывных функций на $[0,1]$ не принадлежит $\mathcal{B}(\mathbb{R}^{[0,1]})$, поскольку имеет мощность лишь континуум.
Это правильное рассуждение?