Просто это неверное утверждение про ОДЗ. Посторонние корни появляются при неэквивалентных преобразованиях уравнения. Неэквивалентные преобразования могут терять корни, могут добавлять корни, поэтому к ним нужен индивидуальный подход. Часто преобразование, являющееся неэквивалентным без учёта ОДЗ, становится эквивалентным при учёте ОДЗ, но это не обязательно так для любого преобразования.
Например, ваш случай: уравнение

,

и уравнение, получающееся возведением в квадрат:

. Они неэквивалентны, так как последнее эквивалентно следующему:

Видно что по сути при возведении мы заменили исходное уравнение объединением двух уравнений, одно из которых — наше, а другое — постороннее, которое и даёт посторонний корень.
Как с этим бороться? Один из вариантов — отсев корней (работает, потому что возведение в квадрат только добавляет посторонние корни). Другой следующий.
Заметим, что

. Значит если мы добавим к нашему уравнению в систему неравенство
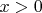
, мы не потеряем и не приобретём корней:

Система

несовместна, поэтому можно объединить её с нашей. Получим

Общую часть

двух объединённых систем можно вынести, получится:

Вот мы и получили объединение двух уравнений, эквивалентное исходному уравнению, возведённому в квадрат. Поэтому это эквивалентно

Вот только такая система с дополнительным неравенством получается эквивалентна исходному уравнению

.
В более общем случае можно доказать, что переход от уравнения

к

является эквивалентным преобразованием только если

— монотонная функция. Функция

немонотонна на

— сначала убывает, потом возрастает. Если повезло и ОДЗ такой, что

или

, то на таком ОДЗ функция возведения в квадрат монотонна, поэтому возведение в квадрат можно делать. Если с ОДЗ не повезло (как в случае выше), то придётся выкручиваться — пример показан выше.