Зачем, интересно, экспонента в знаменателе, чтоб никто не догадался?

Уже для

ответ через

выражаться не будет. Рассмотрев для этого случая функции

, получим, что ответ равен
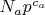
. Изменяя

можно получать разные показатели

. Я думаю, аналогичное утверждение справедливо для любого

.
Интегрирование по частям дает

, если это чем-нибудь поможет.