А в виде башни пентаций g1 это:
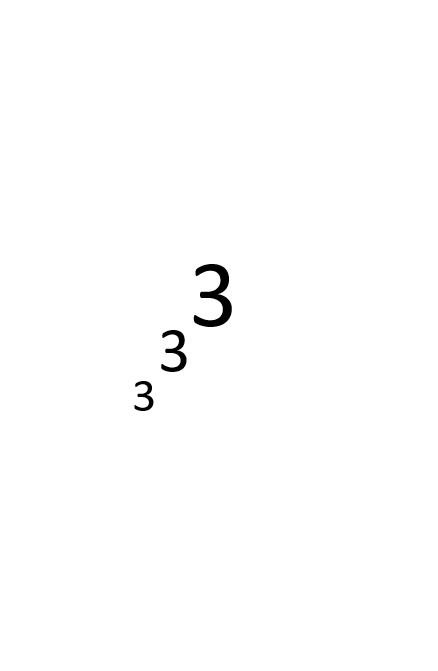
Доброго времени суток. Итак, продолжаю свои упражнения в гугологии. Если

это пентационная башня из трёх троек, то

это пентационная башня из трёх

, то есть пентационная башня из всего лишь девяти троек? И тогда

невообразимо меньше чем

? Я верно рассудил?
Или может быть

невообразимо меньше даже пентационной башни из девяти троек? Подобно тому как

многократно меньше чем степенная башня из четырёх троек

?