Proving the convergence of sequence of Riemann sum.

[Knight2023]

I want to prove that if $f:[a,b] \to \mathbf{R}$ is a bounded continuous function then the sequence of Riemann sum (as the partition is getting finer and finer) converges.

My attempt:

If we can prove that Riemann sum is a Cauchy sequence (sequence as the partition is getting finer and finer), then uniqueness of limit ensures that it converges.

Let $P^{(n)} = \left( \{[x_i^{(n)}, x_{i+1}^{(n)}]\}, t_i^{(n)} \in [x_i^{(n)}, x_{i+1}^{(n)}]\right)$ be a sequence of partitons. Such that:

$$ \lim_{n\to \infty} ||P^{(n)}||= 0 $$

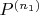
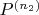
Consider a partition $P^{(n_1)}$ and its refinement $P^{(n_2)}$, that is the latter is obtained by inserting more points in between the points of the former.

Let us try to obtain Cauchy criterion:

$$ \big| \sum_{i=1}^{n_2} f(t_i^{(n_2)}) (x_i^{(n_2)} - x_{i-1}^{(n_2)}) - \sum_{i=1}^{n_1} f(t_i^{(n_1)}) (x_i^{(n_1)} - x_{i-1}^{(n_1)})\big| $$

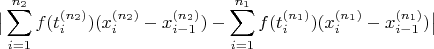
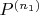
As $P^{(n_1)}$ is coarser, we can take its norm and get an inequality:

$$ \big| \sum_{i=1}^{n_2} f(t_i^{(n_2)}) (x_i^{(n_2)} - x_{i-1}^{(n_2)}) - \sum_{i=1}^{n_1} f(t_i^{(n_1)}) (x_i^{(n_1)} - x_{i-1}^{(n_1)})\big| \leq \big| \sum_{i=1}^{n_2} f(t_i^{(n_2)}) - \sum_{i=1}^{n_1} f(t_i^{(n_1)}) \big| ||P^{(n+1)}|| $$

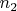
I’m having issues in getting an upper bound for $\sum_{i=1}^{n_2} f(t_i^{(n_2)}) - \sum_{i=1}^{n_1} f(t_i^{(n_1)})$ because one of the sum goes upto $n_2$ while the other upto $n_1$.

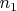
Can you please give me a hint and carry me on over this?

[Dan B-Yallay]

Knight2023 в сообщении #1619729 писал(а):

I’m having issues in getting an upper bound for $\sum_{i=1}^{n_2} f(t_i^{(n_2)}) - \sum_{i=1}^{n_1} f(t_i^{(n_1)})$ because one of the sum goes upto $n_2$ while the other upto $n_1$.

There is no upper bound for that in general. Concider costant function $f(x) = 1$ and the uniform partitioning of $[a, b]$ by powers of 2.

[ihq.pl]

Dan B-Yallay в сообщении #1619784 писал(а):

There is no upper bound for that in general

и то, что справа в неравенстве у ТС, похоже, не сходится к нулю как в общем, так и в частности. Я прав?

[Dan B-Yallay]

ihq.pl
Я сильно не вникал, возможно для того неравенства так и есть.

У него еще проблема в том, что критерий Коши как-то странно выписан. Он ведь рассматривает разницу двух соседних разбиений. А если выписать корректно, тогда точно получится, что невозможно устремить правую часть к нулю.

[Knight2023]

Dan B-Yallay в сообщении #1619795 писал(а):

ihq.pl
Я сильно не вникал, возможно для того неравенства так и есть.

У него еще проблема в том, что критерий Коши как-то странно выписан. Он ведь рассматривает разницу двух соседних разбиений. А если выписать корректно, тогда точно получится, что невозможно устремить правую часть к нулю.

Then how do we prove that the sequence of Riemann sum converges?

[ihq.pl]

Можно воспользоваться тем, что для непрерывной на $[a,b]$ функции

$$\lim_{n\to \infty}\sup_{[x^{(n)}_i,x^{(n)}_{i+1})} f(x) = \lim_{n\to \infty}\inf_{[x^{(n)}_i,x^{(n)}_{i+1})} f(x).$$

[Dan B-Yallay]

Knight2023 в сообщении #1619808 писал(а):

Then how do we prove that the sequence of Riemann sum converges?

Most decent (advanced) Calc books should provide such proof. If my demencia serves me right, one has to resort to use upper and lower Darboux sums, show that they contain Riemann sums in between, then show that they converge and therefore so does Riemann sum - by squeeze theorem. For your specific case you will also have to use uniform continuity of a function, which is continuous on a closed interval.

Something like that is explained on Riemann integral wiki page, but I can not comment how thorough it is.