Линейное пространство. Определение.

[toreto]

Есть вот такая задача. Как ее можно было бы решить теоретически? Сможете помочь разобраться, пожалуйста. Я не уверен в своих ответах.

Определите - какие из перечисленных множеств являются линейными векторными пространствами, а какие - не являются. Ответ нужно обосновать. В скобках я написал свой ответ и обоснование).

1) Множество матриц 2x2 с целочисленными элементами (вроде бы всем 8 аксиомам удовлетворяет).

2) Множество матриц 2x2 с отрицательными элементами (мне кажется, что точно не подходит, так как нет нулевой матрицы из этого же множества)

3) Множество векторов 4x1, координаты которых целые числа (вроде бы всем 8 аксиомам удовлетворяет)

4) Множество векторов 4x1, координаты которых иррациональные числа (мне кажется, что точно не подходит, так как нет нулевого вектора из этого же множества)

5) Множество векторов 3x1, у которых первая координата - ноль (вроде бы всем 8 аксиомам удовлетворяет).

6) Множество векторов 4x1, у которых первая координата - единица (мне кажется, что точно не подходит, так как нет нулевого вектора из этого же множества)

7) Множество верхнетреугольных матриц 2x2 (вроде бы всем 8 аксиомам удовлетворяет).


Определение линейного пространства:

Цитата:

Линейное (векторное) пространство - это множество $ V $ произвольных элементов, называемых векторами, в котором определены операции сложения векторов и умножения вектора на число. Любым двум векторам $ \mathbf{u} $ и $ \mathbf{v} $ поставлен в соответствие вектор $ \mathbf{u} + \mathbf{v} $, называемый суммой векторов $ \mathbf{u} $ и $ \mathbf{v} $, любому вектору $ \mathbf{v} $ и любому числу $ \lambda $ из поля действительных чисел $ \mathbb{R} $ поставлен в соответствие вектор $ \lambda \mathbf{v} $, называемый произведением вектора $ \mathbf{v} $ на число $ \lambda $.

1. $ \mathbf{u} + \mathbf{v} = \mathbf{v} + \mathbf{u} \,~\forall \mathbf{u}, \mathbf{v} \in V $ (коммутативность сложения);
2. $ \mathbf{u} + (\mathbf{v} + \mathbf{w}) = (\mathbf{u} + \mathbf{v}) + \mathbf{w} \,~\forall \mathbf{u}, \mathbf{v}, \mathbf{w} \in V $ (ассоциативность сложения);
3. Существует такой элемент $ \mathbf{o} \in V $, называемый нулевым вектором, что $ \mathbf{v} + \mathbf{o} = \mathbf{v} \,~\forall \mathbf{v} \in V $;
4. Для каждого вектора $ \mathbf{v} $ существует такой вектор $ (-\mathbf{v}) \in V $, называемый противоположным вектору $ \mathbf{v} $, что $ \mathbf{v} + (-\mathbf{v}) = \mathbf{o} $;
5. $ \lambda (\mathbf{u} + \mathbf{v}) = \lambda \mathbf{u} + \lambda \mathbf{v} \,~\forall \mathbf{u}, \mathbf{v} \in V, ~\forall \lambda \in \mathbb{R} $;
6. $ (\lambda + \mu) \mathbf{v} = \lambda \mathbf{v} + \mu \mathbf{v} \,~\forall \mathbf{v} \in V, ~\forall \lambda, \mu \in \mathbb{R} $;
7. $ \lambda (\mu \mathbf{v}) = (\lambda \mu) \mathbf{v} \,~\forall \mathbf{v} \in V, ~\forall \lambda, \mu \in \mathbb{R} $;
8. $ 1 \cdot \mathbf{v} = \mathbf{v} \,~\forall \mathbf{v} \in V $.

[svv]

Пара замечаний. Во-первых, это определение отличается от общего тем, что в нём фиксировано поле скаляров — это $\mathbb R$. Но Вы наверняка знаете, что векторные пространства рассматриваются и над другими полями, например, полем комплексных чисел $\mathbb C$.

Во-вторых, тут

toreto в сообщении #1618994 писал(а):

Линейное (векторное) пространство - это множество $ V $ произвольных элементов, называемых векторами, в котором определены операции сложения векторов и умножения вектора на число. Любым двум векторам $ \mathbf{u} $ и $ \mathbf{v} $ поставлен в соответствие вектор $ \mathbf{u} + \mathbf{v} $, называемый суммой векторов $ \mathbf{u} $ и $ \mathbf{v} $, любому вектору $ \mathbf{v} $ и любому числу $ \lambda $ из поля действительных чисел $ \mathbb{R} $ поставлен в соответствие вектор $ \lambda \mathbf{v} $, называемый произведением вектора $ \mathbf{v} $ на число $ \lambda $.

хотелось бы сделать акцент на том, что результаты этих двух операций тоже должны быть элементами $V$. Можете считать это требование «нулевой», самой важной, аксиомой (об этом часто забывают).

А теперь в 1) возьмём $\lambda=3.87\in\mathbb R$ и $\mathbf v=\begin{bmatrix}1&0\\0&1\end{bmatrix}\in V$. Что с $\lambda\mathbf v$?

[Dedekind]

В принципе верно, кроме вот этого.

toreto в сообщении #1618994 писал(а):

1) Множество матриц 2x2 с целочисленными элементами (вроде бы всем 8 аксиомам удовлетворяет).

toreto в сообщении #1618994 писал(а):

3) Множество векторов 4x1, координаты которых целые числа (вроде бы всем 8 аксиомам удовлетворяет)

У Вас же векторное пространство над полем действительных чисел, правильно?

[toreto]

svv в сообщении #1618995 писал(а):

А теперь в 1) возьмём $\lambda=3.87\in\mathbb R$ и $\mathbf v=\begin{bmatrix}1&0\\0&1\end{bmatrix}\in V$. Что с $\lambda\mathbf v$?

Спасибо. Но ведь ни одна из восьми аксиом в явном виде не утверждает, что результат должен принадлежать тому же векторному пространству. Или я что-то не так понимаю? Точно ли есть эта самая нулевая аксиома?

svv в сообщении #1618995 писал(а):

Пара замечаний. Во-первых, это определение отличается от общего тем, что в нём фиксировано поле скаляров — это $\mathbb R$. Но Вы наверняка знаете, что векторные пространства рассматриваются и над другими полями, например, полем комплексных чисел $\mathbb C$.

Понял, спасибо. Да, нужно учитывать это обстоятельство. Давайте над полем вещевственных чисел.

Dedekind в сообщении #1618996 писал(а):

У Вас же векторное пространство над полем действительных чисел, правильно?

По всей видимости - да. Если над полем целых чисел, то 1 и 3 подходит, а если над полем вещественных, то не подходит по "нулевой" аксиоме о замкнутости операции сложения и умножения на число (если так можно выразиться, правильно ли?)

[svv]

toreto в сообщении #1618998 писал(а):

Точно ли есть эта самая нулевая аксиома?

Точно. В каких-то источниках это выражено лучше, в каких-то хуже. Хорошо, например, в Википедии:

Цитата:

$\bullet$ Определена операция '''сложения''' векторов $V \times V \to {\color{magenta}V}$, сопоставляющая каждой паре элементов $\mathbf{x}, \mathbf{y}$ множества $V$ единственный элемент множества ${\color{magenta}V}$, называемый их '''суммой''' и обозначаемый $\mathbf{x} + \mathbf{y}$.
$\bullet$ Определена операция '''умножения векторов на скаляры''' $F \times V \to {\color{magenta}V}$, сопоставляющая каждому элементу $\lambda$ поля $F$ и каждому элементу $\mathbf{x}$ множества $V$ единственный элемент множества ${\color{magenta}V}$, обозначаемый $\lambda \cdot \mathbf{x}$ или $\lambda \mathbf{x}$.

-- Пн ноя 20, 2023 23:42:53 --

toreto в сообщении #1618998 писал(а):

Если над полем целых чисел

А «поле целых чисел» — поле ли?

[Dedekind]

toreto в сообщении #1618998 писал(а):

По всей видимости - да. Если над полем целых чисел, то 1 и 3 подходит, а если над полем вещественных, то не подходит по "нулевой" аксиоме о замкнутости операции сложения и умножения на число (если так можно выразиться, правильно ли?)

Про вещественные правильно. Но, как уже сказал svv, целые числа - это не поле, а кольцо. Соответственно, и структура над ними будет не векторным пространством, а модулем. https://ru.wikipedia.org/wiki/%D0%9C%D0 ... 0%BE%D0%BC

[dgwuqtj]

toreto в сообщении #1618998 писал(а):

Но ведь ни одна из восьми аксиом в явном виде не утверждает, что результат должен принадлежать тому же векторному пространству.

В алгебре операциями называются отображения вида $X_1 \times \ldots \times X_n \to Y$, если в самом общем случае. В любом определении алгебраической структуры сначала фиксируются множества (скажем, $V$ и $\mathbb R$), потом фиксируются названия и сигнатуры отображений (как процитировал svv), и только в конце накладываются аксиомы. Если вы знакомы с логикой, то это обычная (возможно, многосортная) теория первого порядка без предикатных символов. То есть в математике аксиомы в принципе всегда имеют такого рода "контекст".

[EminentVictorians]

toreto в сообщении #1618994 писал(а):

1) Множество матриц 2x2 с целочисленными элементами (вроде бы всем 8 аксиомам удовлетворяет).

2) Множество матриц 2x2 с отрицательными элементами (мне кажется, что точно не подходит, так как нет нулевой матрицы из этого же множества)

3) Множество векторов 4x1, координаты которых целые числа (вроде бы всем 8 аксиомам удовлетворяет)

4) Множество векторов 4x1, координаты которых иррациональные числа (мне кажется, что точно не подходит, так как нет нулевого вектора из этого же множества)

5) Множество векторов 3x1, у которых первая координата - ноль (вроде бы всем 8 аксиомам удовлетворяет).

6) Множество векторов 4x1, у которых первая координата - единица (мне кажется, что точно не подходит, так как нет нулевого вектора из этого же множества)

7) Множество верхнетреугольных матриц 2x2 (вроде бы всем 8 аксиомам удовлетворяет).


Определение линейного пространства:

Вас правда заставили проверять все эти 7 пунктов прямо по определению линейного пространства? Кошмар. Должна же быть какая-то, я не знаю, лень что ли. Здесь она однозначно будет полезна.

Определением ЛП можно не пользоваться.

Сначала докажем такую лемму.
Пусть $V(K)$ - векторное пространство над полем $K$ и $X$ - произвольное множество. Тогда множество $V^X$ всех функций из $X$ в $V$ само является векторным пространством (над $K$) относительно покомпонентных операций сложения и умножения на скаляр.

Во всех этих 7-ми пунктах речь идет о матрицах. (Под "вектором $4 \times 1$" я понимаю так, что имеют в виду матрицу $4 \times 1$).
Любая матрица - это функция.
Здесь все матрицы обычные, т.е. просто функции из декартова произведения начальных отрезков натурального ряда в поле.
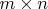
Поэтому, при заданной размерности $m \times n$ все матрицы данной размерности с элементами из поля $K$ образуют ЛП над $K$.

А далее просто берем и проверяем, образуют ли множества из этих 7 пунктов подпространства в соответствующих пространствах матриц. Для этого достаточно проверить замкнутость относительно сложения и умножения на скаляр. И все! Проверять по 8 аксиом на каждый пункт не надо.

По поводу $\mathbb Z$ - поле или не поле. По-моему, тут везде зафиксировано поле $\mathbb R$. Целочисленные матрицы рассматриваются не над $\mathbb Z$, а над $\mathbb R$, поэтому вспоминать про модули не обязательно.

[mihaild]

toreto в сообщении #1618998 писал(а):

Но ведь ни одна из восьми аксиом в явном виде не утверждает, что результат должен принадлежать тому же векторному пространству

В Вашем определении это утверждается (не очень хорошо) еще до аксиом

toreto в сообщении #1618994 писал(а):

множество $ V $ произвольных элементов, называемых векторами

toreto в сообщении #1618994 писал(а):

любому вектору $ \mathbf{v} $ и любому числу $ \lambda $ из поля действительных чисел $ \mathbb{R} $ поставлен в соответствие вектор $ \lambda \mathbf{v} $

(жирный шрифт мой - mihaild)

[Утундрий]

Ну, обуяло человека сомнение. Бывает. Читает, скажем, такой человек определение вроде

Цитата:

Суммой двух чисел называется такое число, что...

и тут же сомневаться начинает. А одинакового ли рода число с теми, из которых построено? А они сами по себе одного рода? А как понимать "называется"?

[toreto]

svv в сообщении #1619000 писал(а):

Точно. В каких-то источниках это выражено лучше, в каких-то хуже. Хорошо, например, в Википедии
:

Спасибо, понял!

svv в сообщении #1619000 писал(а):

А «поле целых чисел» — поле ли?

Нет, не поле. Мой промах, спасибо, что поправили.

Dedekind в сообщении #1619002 писал(а):

Про вещественные правильно. Но, как уже сказал svv, целые числа - это не поле, а кольцо. Соответственно, и структура над ними будет не векторным пространством, а модулем. https://ru.wikipedia.org/wiki/%D0%9C%D0 ... 0%BE%D0%BC

Этого я не знал, спасибо, буду иметь ввиду.

EminentVictorians в сообщении #1619050 писал(а):

Сначала докажем такую лемму.

Спасибо большое за лемму!
Альтернатива использованию Вашей леммы - это прогонять все 8 аксиом, зная заранее, что ответ будет да? (речь про множества, которые являются линейными пространствами). Те, что не являются, для них достаточно просто контрпримера.

[EminentVictorians]

toreto в сообщении #1619064 писал(а):

Альтернатива использованию Вашей леммы - это прогонять все 8 аксиом, зная заранее, что ответ будет да? (речь про множества, которые являются линейными пространствами).

Я имею в виду, что здесь Вам очень повезло. Операции сложения и умножения на число для матриц определены так как они определены ровно потому что матрицы - это функции, и мы хотим чтобы была согласованность операций над матрицами с покомпонентными операциями для них как функций.

Для умножения матриц такого уже не будет. Умножение матриц определено не как покомпонентное умножение их как функций. Там другая мотивация - согласованность с композицией линейных операторов.

Возьмите, например, пункт 7 с верхнетреугольными матрицами.
Сумма двух верхнетреугольных матриц верхнетреугольная? Да.
Произведение верхнетреугольной на действительное число - верхнетреугольная? Да.
Все. Значит они образуют векторное пространство (подпространство в пространстве всех матриц $2 \times 2$; хотя здесь даже привязываться к размерности не обязательно, можно было бы и про $n \times n$ говорить).
Как видите, проверять 8 аксиом не пришлось.