Текстовая задача. Формула включений-исключений

[lele174]

Среди абитуриентов, выдержавших приемные экзамены в ВУЗ, оценку 'отлично' получили: по математике — 48 абитуриентов, по физике — 37, по русскому языку — 42, по математике или физике — 75, по математике или русскому языку — 66, по всем трем предметам — 4. Сколько абитуриентов получили хотя бы одну пятерку? Сколько среди них получивших только одну пятерку?

Добрый день! Не мог решить задачу 5 часов, решил перебором. Ответ не сошелся, мне кажется, что в ответе ошибка. Ответ в учебнике 94, 65. Но мое решение показывает, что такой ответ не подходит. Пожалуйста, помогите разобраться. У меня впечатление, что эту задачу невозможно решить другим способом. Только перебрать значения на глаз

По формуле включений-исключений у меня получилось, что сумма {абитуриенты с хотя бы одной пятеркой} и {абитуриенты с пятеркой по физике и по русскому} равна девяносто семи. Еще я нашел, что разница между {абитуриенты с пятеркой только по физике} и {абитуриенты с пятеркой только по русскому} равна девяти, а в множестве {абитуриенты с пятеркой только по математике} 18 элементов. По этим данным я перебрал возможные значения {абитуриенты, получившие 'отлично' только по физике} и {абитуриенты, получившие 'отлично' только по русскому}, со второго раза угадал значения 22 и 13.

В ответе у меня 53, 88. Мне кажется, что я получил верный ответ, но я не могу понять, как прийти к нему без перебора возможных значений неизвестных.

Простите, пожалуйста, я сейчас учусь пользоваться синтаксисом.

[dgwuqtj]

Так в этой задаче не единственный ответ. Можно при желании найти все ограничения, которым удовлетворяют количества студентов с пятёрками по всем наборам предметов (не забудьте, что они целые и неотрицательные).

[lele174]

dgwuqtj в сообщении #1615598 писал(а):

Так в этой задаче не единственный ответ. Можно при желании найти все ограничения, которым удовлетворяют количества студентов с пятёрками по всем наборам предметов (не забудьте, что они целые и неотрицательные).

Я вчера догадывался, что решений может быть несколько. Как можно найти ограничения? Система уравнений с тремя неизвестными, видимо. Спасибо!

[dgwuqtj]

Там 7 неизвестных: количество абитуриентов с пятёркой только по математике, только по математике и физике, и т.д. Уравнения на них даны в условии (останется 1 степень свободы), к тому же все они являются целыми неотрицательными.

[Booker48]

lele174
Проверьте условие. В сети эта задача встречается, но с добавлением "по физике или по русскому языку - 76 человек".

[EUgeneUS]

Кстати, а как в таких задачах нужно трактовать "или", как OR или как XOR?

[lele174]

EUgeneUS в сообщении #1615636 писал(а):

Кстати, а как в таких задачах нужно трактовать "или", как OR или как XOR?

В этой задаче 'или' это OR, объединение множеств

[svv]

lele174 в сообщении #1615573 писал(а):

Среди абитуриентов, выдержавших приемные экзамены в ВУЗ, оценку 'отлично' получили: по математике — 48 абитуриентов, по физике — 37, по русскому языку — 42, по математике или физике — 75, по математике или русскому языку — 66, по всем трем предметам — 4.

На левой картинке показана информация, которую можно отсюда извлечь:

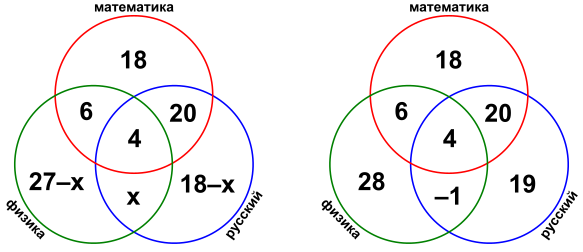
Получаем, что
$93-x$ студентов получили хоть одну пятёрку;
$63-2x$ студентов получили ровно одну пятёрку;
$75-x$ студентов получили пятёрку по физике или русскому.

Учитывая любое из дополнительных условий:
$\bullet$ в ответе сказано, что $94$ студента получили хоть одну пятёрку,
$\bullet$ в ответе сказано, что $65$ студентов получили ровно одну пятёрку,
$\bullet$ согласно Booker48, в сети пишут, что $76$ студентов получили пятёрку по физике или русскому,
находим $x=-1$. Это число студентов, сдавших на «отлично» физику и русский, но не математику. Уважаемые участники, не понимаю вашего удивления, вы что, отрицательного человека никогда не видели? Обратите внимание на замечательное согласие всех дополнительных условий.

С этой дополнительной информацией получаем на кругах Венна раскладку, как на правой картинке. Проверьте, пожалуйста, выполнение всех требований, включая дополнительные.

[EUgeneUS]

svv в сообщении #1615967 писал(а):

С этой дополнительной информацией получаем на кругах Венна раскладку, как на правой картинке. Проверьте, пожалуйста, выполнение всех требований

ИМХО, есть разница в трактовке предлога "ИЛИ".
Выше ТС сказал:

lele174 в сообщении #1615639 писал(а):

В этой задаче 'или' это OR, объединение множеств

А Вы какой вариант использовали при решении?

[svv]

OR.

[EUgeneUS]

Проверил с XOR, получается минус два с половиной землекопа (где у Вас минус один)

[svv]

И тоже нормальный вариант, мультфильм, я думаю, все смотрели.