IndexOutOfRangeА как, например, получается, что все три должны ждать? Т.е. P(3W)? Разве минимум один рабочий не работает в любых обстоятельствах?
Если задача стоит так: "Три человека взяли по случайному шару. Какова вероятность, что все шары разные?", то правильный ответ

. Но если совпадение есть, то оно может быть парным или тройным. В первом случае будет ждать один рабочий, во втором - два. Если за коллизию считать число ждущих рабочих в цикле, то да, нужно считать немного аккуратнее.
3W означает, что ждет рабочий под номером 3, а не то, что 3 рабочих одновременно ждут. И да, я по сути посчитал для 3 действий, берет 1-ый рабочий, берет 2-ой рабочий, берет 3-ий рабочий, но действия бесконечны. И интересует в среднем количество коллизий в такой системе. Даже упростим задачу - если рабочий ждет, то он ждет ровно момента завершения работы другого рабочего (чтобы исключить влияение ожидания и выровнять всех рабочих во временной сетке)
-- 06.10.2023, 14:02 --Так как количество действий бесконечно, то начальным моментом, когда рабочие начинают брать шары можно пренебречь. Нас интересует вероятность того, что рабочий возьмет шар с номером, который уже в обработке. Если у нас

рабочих и какой-то из рабочих пытается взять шар с номером

, то по сути вероятность коллизии - это вероятность того, что шар

взят в обработку или находится в ожидании у хотя бы одного из остальных
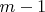
рабочих.
То есть на каждом цикле имеем систему из 3 значений, где 3A - означает, что шар с номером 3 находится в обработке, а 5W - означает, что шар с номером 5 находит в ожидании на обработку.
Тогда на каждом цикле система выглядит как

. S в данном случае это либо A, либо W. Потом каждый из рабочих пытается либо взять следующий шар в обработку, либо попытается обработать шар, который был в ожидании. Вроде бы не имеет значение в каком порядке они будут это делать, так что допустим от рабочего с номером 1 до рабочего с номером 3. Вопрос, какое количество W мы в среднем имеем на каждой итерации?