Корреляция скоростей взаимодействующих частиц

[Knight7]

Читаю §13.3.2 в книге "Mark E. Tuckerman, Statistical Mechanics: Theory and Molecular Simulation". Там автор выводит формулу Грина-Кубо для коэффициента диффузии. Смысла вывода в том, что к Гамильтониану исходной системы

$$ H=\sum_{i}\frac{\mathbf{p}_{i}^{2}}{2m_{i}}+U\left(\mathbf{r}_{1},\dots,\mathbf{r}_{N}\right) $$

можно добавить член внешней постоянной силы $-f\sum_{i}x_{i}$. Далее, полагая, что внешний потенциал достаточно слаб, можно линеаризовать выражение для концентрации частиц (которая распределяется по Больцману) и воспользоваться результатом для вывода скорости дрейфа частиц (с помощью закона Фика). Таким образом, коэффициент диффузии можно записать так:

$$ D=\int_{0}^{\infty}\frac{1}{N}\left\langle \left(\sum_{i}\dot{x}_{i}\left(0\right)\right)\left(\sum_{i}\dot{x}_{i}\left(t\right)\right)\right\rangle dt $$

Однако далее он пишет:

Цитата:

В термодинамическом равновесии, распределение скоростей (импульсов) частиц является произведением независимых гауссовских распределений. Отсюда следует $\left\langle \dot{x}_{i}\dot{x}_{j}\right\rangle =0$ а также то, что $\left\langle \dot{x}_{i}\left(0\right)\dot{x}_{j}\left(t\right)\right\rangle =0$ для $i\neq j$.

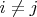
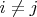
Если с первым утверждением еще можно согласиться, то со вторым (то, что $\left\langle \dot{x}_{i}\left(0\right)\dot{x}_{j}\left(t\right)\right\rangle =0$ для $i\neq j$) есть вопросы. Я смог доказать для себя данное утверждение с помощью уравнения Ланжевена, полагая, что шумовые члены разных частиц не коррелируют между собой. Однако данный вывод опирается на предположении, что частицы не взаимодействуют между собой. Если же частицы взаимодействуют, то я не вижу никаких причин почему величина $\left\langle \dot{x}_{i}\left(0\right)\dot{x}_{j}\left(t\right)\right\rangle$ должна быть равна нулю. Понятно, что в пределе $t\to\infty$ корреляция скоростей должна убывать, но почему это справедливо для любого временного интервала?