paranoidandroidПосмотрите на задачу ещё так.
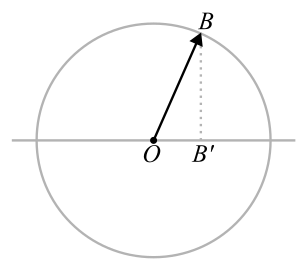
У Вас есть стрелка длиной

. Конец стрелки (точка

) равномерно вращается по окружности с центром

. Период вращения равен

. Тогда проекция конца стрелки (точка

) на горизонтальную ось совершает гармонические колебания с амплитудой

и периодом

, как в условии задачи. Можно считать, что

— это брусок.
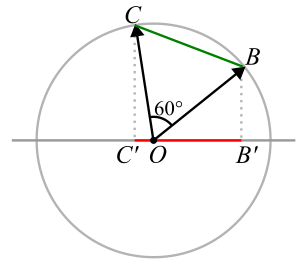
За время

стрелка проходит шестую часть окружности, то есть

. Моментам времени

и

отвечают два положения стрелки

и

, угол между которыми

(и, соответственно, два положения бруска

и

). Расстояние, которое пройдёт брусок за время от

до

, равно длине отрезка

, то есть проекции отрезка

на горизонтальную ось.
Треугольник
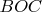
равнобедренный. А поскольку

, он ещё и равносторонний. Поэтому

.
Теперь представьте, что
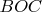
вращается вокруг

, как жёсткая конструкция. Когда длина

будет максимальна? Когда отрезок

горизонтален. В этом случае

.