Хотелось бы поделиться с форумчанами одной загадкой, которую отправлял когда-то в телевизионное ЧГК (во времена, когда еще верил в чудеса, т.е. в то, что присланные вопросы могут принять для игры).
Даны четыре фигуры. Какая фигура является лишней?
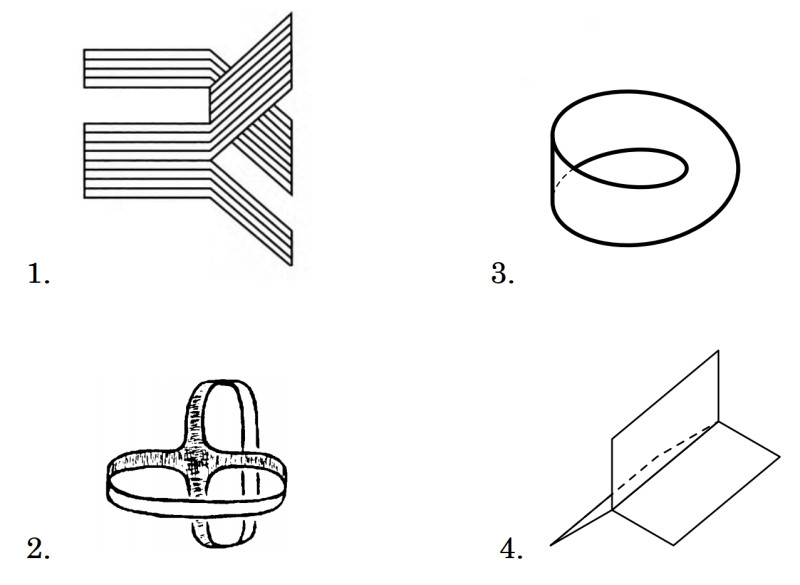
(Присланная в ЧГК формулировка)
Перед вами изображение с четырьмя фигурами. Представив себе обычный лист бумаги, ответьте, какая фигура является лишней.
(Подсказки и комментарии)
Конечно, это не строго математическая задача, и этим она схожа со всякими "угадай что имел в виду автор", но имхо, она лучше большинства подобных загадок, т.к. в присланной формулировке есть прямой намек на конкретный ответ с конкретным обоснованием (лишняя - первая). Формулировка на форуме не содержит этого намека, а потому уже более чем допускает в качестве ответа любую из фигур, и каждое из обоснований может быть строгим математическим, поэтому если ответ не совпадает с "авторским", то это, естественно, ничего не говорит о его (не)корректности, пока есть хорошее обоснование этого ответа. В этом смысле я не настаиваю, что мой предполагаемый ответ чем-то лучше другого ответа с обоснованием - было бы интересно посмотреть, что придумают другие.