Есть у меня пара вопросов по поводу строгого вывода нескольких понятий в теории вероятностей. Я понимаю, что тут хорошо бы сесть и с нуля это всё разбирать по книгам из теории меры, но к сожалению, сейчас физически нет на это времени. Хотелось бы получить хотя бы базовую интуицию "а почему это законно", чтобы хотя бы без недоверия можно было работать с этими объектами.
Первый вопрос касается смешанных распределений, второй условных распределений/формулы Байеса в общем виде, но там даже сформулировать "претензии" тяжеловато, начну с первого вопроса.
Стандартное "определение" которое я видел для самой примитивной случайной величины

, имеющей смешанное распределение, выглядит как-то так:

Опишу какую-то свою интуицию по поводу случайных величин. Начну с того что, главный объект, связанный со случайной величиной

, это индуцированная ею мера
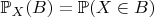
для всякого борелевского множества

. Ну и засчёт этого у нас всегда с корректно определённой случайной величиной можно связать тройку

. Весь вопрос, как эту самую меру индуцировать.
Я в какой-то мере привык, что случайные величины имеются двух типов -- дискретные случайные величины и непрерывные случайные величин.
Для дискретных случайных величин всё вообще замечательно, меру можно задать поточечно, поэтому удобно вести функцию вероятности (probability mass function)

.
А непрерывной случайной величиной мы называем случайную величину, для которой индуцируемую ею меру можно задать с помощью интеграла от функции
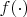
, называемой функцией плотности вероятности : для всякого борелевского множества

, причём эта функция должна быть неотрицательна и интеграл от неё по всей вещественной прямой должен равняться

.
Далее мы говорим, что есть универсальный способ описания мер -- через функции распределения. Есть теорема, которая говорит, что по каждой корректно заданной функции распределения можно однозначно восстановить меру.
И если я правильно понимаю, то законность существования смешанных распределений гарантирует именно функция распределения.
Для случайной величины

имеющей вид, заданный выше, попробуем вывести её функцию распределения.
Пусть событие

заключается в том что случайная величина

равна случайной величине

, событие

-- заключается в том что случайная величина

равна случайной величине

. Верно ли я понимаю, что мы сами, так сказать, из условия задачи знаем, что

и

? Также мы сами говорим, что третьего не дано -- а значит это разбиение пространства элементарных исходов, которое, как я понимаю, в этом случае

Тогда можно ввести ещё третье событие
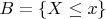
для некоторого фиксированного

.
По формуле полной вероятности,

.
Тут снова некоторое допущение делаю -- считаю, что раз мы знаем, что как только

, так у

непрерывное распределение, которое было у

, значит

. Такие моменты меня немного смущают. То есть вроде бы и я сам это в условии задаю, а вроде как я это из ниоткуда взял. Ну и считаю по тем же причинам , что

.
Тогда, для каждого

,

.
Вроде как я даже явно могу проверить, что заданная таким образом функция

действительно является функцией распределения, то есть удовлетворяет свойствам функции распределения, например, пределы на бесконечностях у неё правильные.
И несмотря на то что вроде бы я её и получил логичным образом и судя по всему, если просто сразу написать эту формулу, то она чисто формально будет функцией распределения, я всё равно не чувствую уверенности что всё было корректно. Я не нашёл какого-то более менее подробного и не поверхностного материала по смешанным распределениям, хотя очевидно, что они очень полезны на практике и и я регулярно вижу как люди их совершенно спокойно используют.
Поэтому, помимо вопросов, которые я задал по ходу, мне интересно, всё ли у меня верно в моих рассуждениях? Какие-то дальнейшие вопросы тогда спрошу, если кто-то текущие рассуждения прокомментирует, может уже тут проблемы.