Закономерность в раскраске натуральных чисел

[mathematician123]

Натуральные числа от 1 до $m$ раскрашены в $n$ цветов. Раскраска --- функция $f(x)$, которая числу $x$ сопоставляет некоторое число от $1$ до $n$. Верно ли, что при достаточно большом $m$ найдутся натуральные числа $k, l$, такие что числа $l + 1, l + 2 \ldots, l + k$ с точностью до перестановки раскрашены также как и числа $l + k + 1, l + k + 2, \ldots, l + 2k$? 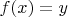То есть, для любого $1 \le y \le n$ уравнение $f(x) = y$ будет иметь одинаковое число решений на промежутках $[l + 1, l + k]$ и $[l + k + 1, l + 2k]$.

Если $n = 2$, то можно взять $m \ge 4$. Действительно, либо $f(1) = f(2)$, либо $f(3) = f(4)$, либо $\{f(1), f(2)\} = \{f(3), f(4) \} = \{1, 2 \}$. Если $n = 3$, то перебором можно показать, что утверждение верно при $m \ge 8$. Верно ли утверждение в общем случае? Нетрудно показать, что $m \ge 2^n$. Контрпример для $m = 2^n - 1$ строится по индукции: 212 при $n = 2$, 3231323 при $n = 3$, при $n = 4$ вставим в эту последовательность 8 четвёрок и т.д. Но это не оптимальная оценка. В случае $n = 4$ можно построить контрпример для $m = 16$: 4143141243124143.