Найдите площадь треугольника

[Rak so dna]

wrest да (точнее бикубическое). Система должна быть:

$\begin{cases} u^2+\frac{uvw}{u+v+w}=x^2\\ v^2+\frac{uvw}{u+v+w}=y^2\\ w^2+\frac{uvw}{u+v+w}=z^2\\ \end{cases}$

Я бы её начал решать так:

Пусть

$\begin{cases} u+v+w=p\\ (u+v)(v+w)(w+u)=q\\ uvw=r\\ x^2+y^2+z^2=A\\ x^2y^2+y^2z^2+z^2x^2=B\\ x^2y^2z^2=C \end{cases}$

тогда

$\begin{cases} \frac{p^3-2q+r}{p}=A\\ \frac{q(q-2r)}{p^2}=B\\ \frac{q^2r}{p^3}=C \end{cases}$

из 2-го и 3-го уравнений получим

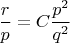
$q^3-Bp^2q-2Cp^3=0$ а значит уже можем найти $\dfrac{q}{p}$, зная это из 3-го уравнения найдём $\dfrac{r}{p}=C\dfrac{p^2}{q^2}$ ну и из 1-го уравнения найдём $p$:

$p^2=2\dfrac{q}{p}-\dfrac{r}{p}+A$

Как не крути, а от кубического уравнения никуда не деться