Уважаемые эксперты.
Представленный ниже материал имеет какие-то принципиальные ошибки, наверное такие же как и в материале в теме "гравиполе куба вдоль диагонали",которые приводят к ошибочному результату, но обнаружить их не удается. Уверен, что "свежий" взгляд их моментально обнаружит. Излагаю материал подробно, нет необходимости отвлекать внимание.
Заранее благодарен.
Силовое воздействие куба(

),на единичную массу, на линии ортогональной грани и проходящей через ее геометрический центр будем находить из выражения:

где:

-объем куба,

-гравитационная постоянная,

- плотность вещества куба,

-удаление контрольной точки от центра масс.
Интегрируем по переменной ( z): Производная по z от выражения

равна

это равно выражению под тройным интегралом. Следовательно:

где:

- полуребро куба. Интегрируем по переменной у:
Согласно таблицам интегралов(Двайт) 200.01:

Модуль сразу заменяем на круглые скобки, так как выражение под модулем, при

много большем

, больше нуля.
где:

-для первого двойного интеграла,

-для второго двойного интеграла. Получим выражение для поля:


Введем обозначения для интегралов в скобках по порядку и будем вычислять их отдельно без произведения

:


Берем по частям:





Рассмотрим вторую интегральную часть выражения

:

Введем переменную

:



, то в новых переменных интеграл будет иметь вид:

Введем новую переменную:

,

. Тогда интеграл будет иметь вид:


коэффициенты квадратного трехчлена под корнем равны:

Согласно таблицам интегралов (Двайт) 380.311

Это равно:

Согласно таблицам(Двайт)380.001


Для реальных

интеграл будет иметь вид:

Следующий интеграл согласно таблицам (Двайт) 380.111

Для реальных

интеграл будет иметь вид:


В этом интеграле возвращаемся к переменной


Переходим к переменной( х) при


Собираем выражение (1):

Возвращаемся к переменной х в первых двух слагаемых:

тогда
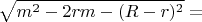


Тогда общий вид выражения (2) в переменных (х) будет иметь вид:

Возвращаемся к выражению

, при интегрировании по частям и добавляем к полученному выше свободное выражение. Таким образом общий вид

в переменной (х) будет иметь вид:?

Найдем


берем по частям










подставим в интеграл, получим:

делаем подстановку

,

,

, получаем:

,

,

,

Согласно таблицам интегралов(Двайт) 380.311:

получится следующее выражение:
![$(-1)[\sqrt{m^2+2rm-(R-r)^2}+\frac{2r}{2}\int\limits_{}^{}\frac{dm}{\sqrt{m^2+2rm-(R-r)^2}}-(R-r)^2\int\limits_{}^{}\frac{dm}{m\sqrt{m^2+2rm-(R-r)^2}}]$ $(-1)[\sqrt{m^2+2rm-(R-r)^2}+\frac{2r}{2}\int\limits_{}^{}\frac{dm}{\sqrt{m^2+2rm-(R-r)^2}}-(R-r)^2\int\limits_{}^{}\frac{dm}{m\sqrt{m^2+2rm-(R-r)^2}}]$](https://dxdy-01.korotkov.co.uk/f/c/d/d/cdd18f20bb520fdd97ca0884e33c406082.png)
Интеграл во втором слагаемом согласно таблицам: 380.001,


,

интеграл в третьем слагаемом согласно таблицам 380.111

,



Подставим в выражение(**):
![$I_2=x\ln(-r+\sqrt{x^2+r^2+(R-r)^2})+(-1)[\sqrt{m^2+2rm-(R-r)^2}+r\ln(2\sqrt{m^2+2rm-(R-r)}+2m+2r)-(R-r)\arcsin\frac{2rm-2(R-r)^2}{m\sqrt{4r^2+4(R-r)^2}}]$ $I_2=x\ln(-r+\sqrt{x^2+r^2+(R-r)^2})+(-1)[\sqrt{m^2+2rm-(R-r)^2}+r\ln(2\sqrt{m^2+2rm-(R-r)}+2m+2r)-(R-r)\arcsin\frac{2rm-2(R-r)^2}{m\sqrt{4r^2+4(R-r)^2}}]$](https://dxdy-02.korotkov.co.uk/f/d/9/d/d9dc643efef4cf68abb8ce016991fdb782.png)
Переходим к переменной t и далее к переменной х:

тогда



продолжение корня

после преобразования

Найдем


берем по частям



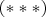


,

, подставим в интеграл, получим:

, замена переменной:

,


,

,

,

Согласно таблицам интегралов(Двайт) 380.311

Интеграл во втором слагаемом согласно таблицам 380.001 равен

:


Интеграл в третьем слагаемом согласно таблицам 380.111

,


тогда

, подставляем в (***)



![$\frac{(R+r)^2}{(R+r)}\arcsin\frac{-2rm-2(R+r)^2}{m\sqrt{4r^2-4(-(R+r)^2))}}]$ $\frac{(R+r)^2}{(R+r)}\arcsin\frac{-2rm-2(R+r)^2}{m\sqrt{4r^2-4(-(R+r)^2))}}]$](https://dxdy-03.korotkov.co.uk/f/e/e/b/eeb9883f4664167f9808b89da74eff1082.png)
, в выражениях в скобках возвращаемся сначала к переменной t, а далее к пер. х, так как






найдем


интегрируем по частям

,




,

,

Подставим в интеграл(****)

,

,

,


,

,

,

Согласно таблицам интегралов(Двайт)380.311:

![$(-1)\int\limits_{}^{}\frac{\sqrt{m^2+2rm-(R+r)^2}}{m}dm=(-1)[\sqrt{m^2+2rm-(R+r)^2}+r\int\limits_{}^{}\frac{dm}{\sqrt{m^2+2rm-(R+r)^2}}-(R+r)^2\int\limits_{}^{}\frac{dm}{m\sqrt{m^2+2rm-(R+r)^2}}]$ $(-1)\int\limits_{}^{}\frac{\sqrt{m^2+2rm-(R+r)^2}}{m}dm=(-1)[\sqrt{m^2+2rm-(R+r)^2}+r\int\limits_{}^{}\frac{dm}{\sqrt{m^2+2rm-(R+r)^2}}-(R+r)^2\int\limits_{}^{}\frac{dm}{m\sqrt{m^2+2rm-(R+r)^2}}]$](https://dxdy-02.korotkov.co.uk/f/9/f/7/9f707bb60dfe3343e3265f375fd3463a82.png)
интеграл второго слагаемого в скобках согласно таблицам 380.001



Интеграл третьего слагаемого в скобках согласно таблицам 380.111

,



Подставляем в выражение(****):


![$-(R+r)\arcsin\frac{2rm-2(R+r)^2}{m\sqrt{4r^2-4(-(R+r)^2)}}]$ $-(R+r)\arcsin\frac{2rm-2(R+r)^2}{m\sqrt{4r^2-4(-(R+r)^2)}}]$](https://dxdy-03.korotkov.co.uk/f/6/9/3/693efb262f5788e3c0f8e8985444655a82.png)
Вернемся к переменной t и далее к х:






Вернемся к напряженности гравиполя

При подстановке пределов для

,

, все члены, где есть арксинус сократятся, т.к.

,

, следовательно останутся:




Х-ы, сокращаются. В оставшемся выражении складываем одинаковые логарифмы:




В слагаемых выносим 2 из под знака логарифма:





После сокращения получим:




поставим пределы интегрирования

,

, получим:

![$+2[r\ln(r+\sqrt{r^2+r^2+(R-r)^2})-r\ln(-r+\sqrt{r^2+r^2+(R-r)^2})]$ $+2[r\ln(r+\sqrt{r^2+r^2+(R-r)^2})-r\ln(-r+\sqrt{r^2+r^2+(R-r)^2})]$](https://dxdy-04.korotkov.co.uk/f/f/7/2/f721e1d17db74fc6403d41e19b24aa7f82.png)
![$-[r\ln(-r+\sqrt{r^2+r^2+(R-r)^2})+r\ln(-r+\sqrt{r^2+r^2+(R-r)^2})]$ $-[r\ln(-r+\sqrt{r^2+r^2+(R-r)^2})+r\ln(-r+\sqrt{r^2+r^2+(R-r)^2})]$](https://dxdy-03.korotkov.co.uk/f/e/d/4/ed45a88ad08ae839872ed16c179f03f982.png)
![$-[r\ln(r+\sqrt{r^2+r^2+(R+r)^2})+r\ln(r+\sqrt{r^2+r^2+(R+r)^2})]$ $-[r\ln(r+\sqrt{r^2+r^2+(R+r)^2})+r\ln(r+\sqrt{r^2+r^2+(R+r)^2})]$](https://dxdy-04.korotkov.co.uk/f/f/2/1/f2167d6b223afd3357d4381459ad24c882.png)
![$-2[r\ln(r+\sqrt{r^2+r^2+(R+r)^2})-r\ln(-r+\sqrt{r^2+r^2+(R+r)^2})]$ $-2[r\ln(r+\sqrt{r^2+r^2+(R+r)^2})-r\ln(-r+\sqrt{r^2+r^2+(R+r)^2})]$](https://dxdy-01.korotkov.co.uk/f/0/1/7/0174fd007e89fb7cc9f85b33706c6bc482.png)

----------------------------------------------------------------------------


Преобразуем с учетом гравитационной постоянной и плотности куба

![$$H=4rG\rho_{k}\ln[\frac{(r+\sqrt{2r^2+(R-r)^2})(-r+\sqrt{2r^2+(R+r)^2})}{(-r+\sqrt{2r^2+(R-r)^2})(r+\sqrt{2r^2+(R+r)^2})}]$$ $$H=4rG\rho_{k}\ln[\frac{(r+\sqrt{2r^2+(R-r)^2})(-r+\sqrt{2r^2+(R+r)^2})}{(-r+\sqrt{2r^2+(R-r)^2})(r+\sqrt{2r^2+(R+r)^2})}]$$](https://dxdy-03.korotkov.co.uk/f/6/f/4/6f48def36a076ce56cb5cebdb0a70d1082.png)
пусть куб с ребром

и шар радиусом

и плотности

, имеют одну и ту же массу:
Тогда плотность шара будет выражаться:
Напряженность гравиполя шара равна:
найдем отношение поля шара к полю куба:
Приведем к единой плотности

:
Введем переменную :
Тогда выражение (*) будет иметь вид:
![$$\frac{H_0}{H_{k}}=\frac{\frac{2}{n^2}}{\ln[\frac{(1+\sqrt{2+(n-1)^2})(-1+\sqrt{2+(n+1)^2})}{(-1+\sqrt{2+(n-1)^2})(1+\sqrt{2+(n+1)^2})}]}$$ $$\frac{H_0}{H_{k}}=\frac{\frac{2}{n^2}}{\ln[\frac{(1+\sqrt{2+(n-1)^2})(-1+\sqrt{2+(n+1)^2})}{(-1+\sqrt{2+(n-1)^2})(1+\sqrt{2+(n+1)^2})}]}$$](https://dxdy-01.korotkov.co.uk/f/0/a/8/0a826fb6a912791fb1f2512125541d0382.png)
Предел этого выражения при

стремящимся к бесконечности равен 0.5:
После упрощения выражение будет иметь вид:
Берем производную от числителя и знаменателя:
То есть на бесконечности куб будет притягивать в два раза сильнее.
Но это ошибочный результат.