Нахождение производной и первообразной с помощью БПФ

[ivantozavrus]

Выдали задание: посчитать производную и первообразную функции с помощью быстрого преобразования Фурье в Matlab. Функция:
$f(x)=1-|x|, |x| \leqslant 1; f(x)=0, |x| >1$ .

Вот код программы:

clear
dt = 0.0001; %дискретизация по времени
t = -1:dt:(1-dt);
size_t = length(t);
syms func x
func = 1 - abs(x);
funcdif = diff(func, x); %символьное дифференцирование

func_val = double(subs(func, {'x'}, [t]));
funcdif_val = double(subs(funcdif, {'x'}, [t])); % подставляем значения в исходную функцию и производную

func_fft = fft(func_val); %БПФ
frq = [0:size_t/2 -size_t/2+1:-dt]/dt/size_t; % частоты (если не ошибаюсь, то fft именно в таком порядке хранит результаты %преобразования).
funcdif_fft = ifft(1i*frq.*func_fft); % вычисляем производную

plot(t, funcdif_val);
hold on
plot(t, funcdif_fft);

funcanti = int(func, x);
funcanti_val = double(subs(funcanti, {'x'}, [t])); % символьно проинтегрировали и подставили значения
funcanti_fft = ifft(func_fft/(1i)./frq); % воспользовались свойствами преобразования Фурье для нахождения первообразной
plot(t, funcanti_val);
hold on
plot(t, funcanti_fft);

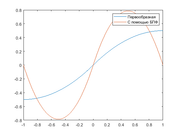
Но, по факту, ничего не выходит. График производной, вычисленной с помощью БПФ, полностью совпадает по форме с реальным графиком, но отличается по амплитуде. А вот с интегралом все совсем плохо. Может кто-нибудь подсказать, как правильно в чем здесь ошибка?