Формулы сокращенного умноженияОбщие формулы:



Простейшие формулы:


 Добавлено спустя 14 минут 23 секунды:Формулы Виета.
Добавлено спустя 14 минут 23 секунды:Формулы Виета.Формулы Виета для приведенного многочлена

-й степени

с корнями

:

Формулы Виета для приведенного квадратного трехчлена

:

Формулы Виета для приведенного кубичного многочлена

:
 Добавлено спустя 8 минут 40 секунд:Корни квадратного уравнения
Добавлено спустя 8 минут 40 секунд:Корни квадратного уравненияФормула вычисления корней квадратного уравнения

с действительными коэффициентами:

Если

, то уравнение имеет два различных действительных корня; если

, то уравнение имеет один действительный корень кратности 2; если

, то
уравнение имеет два комплексно сопряженных корня:

Формула вычисления корней приведенного квадратного уравнения

:

Формула вычисления корней квадратного уравнения с четным вторым коэффициентом

:
 Добавлено спустя 25 минут 7 секунд:Корни кубичного уравнения с действительными коэффициентами.
Добавлено спустя 25 минут 7 секунд:Корни кубичного уравнения с действительными коэффициентами. Корни неполного кубичного уравнения

вычисляются по
формулам Кардано:

где
![$$ A=\sqrt[3]{-\frac{q}{2}+\sqrt{Q}}, \quad B=\sqrt[3]{-\frac{q}{2}-\sqrt{Q}}, \quad Q=\left(\frac{p}{3}\right)^3 + \left(\frac{q}{2}\right)^2,$$ $$ A=\sqrt[3]{-\frac{q}{2}+\sqrt{Q}}, \quad B=\sqrt[3]{-\frac{q}{2}-\sqrt{Q}}, \quad Q=\left(\frac{p}{3}\right)^3 + \left(\frac{q}{2}\right)^2,$$](https://dxdy-03.korotkov.co.uk/f/a/b/d/abdb073155c2a22f4d0dc2ab6d986bef82.png)
причем в качестве

и

выбираются любые значения кубичных корней, удовлетворяющие равенству

.
Корни неполного кубичного уравнения с действительными коэффициентами

могут быть вычислены также по следующим формулам
(тригонометрическое решение).
Если

, то

, и

где значения тригонометрических функций вычисляются по значению

Если

и
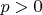
, то

где значения тригонометрических функций вычисляются по значению
![$$ \tg \alpha = \sqrt[3]{\tg \frac {\beta}{2}}, \quad \tg \beta = \frac{2}{q}\sqrt{\left(\frac{p}{3}\right)^3}, \quad |\alpha| \le \frac{\pi}{4}, \quad |\beta| \le \frac{\pi}{2}.$$ $$ \tg \alpha = \sqrt[3]{\tg \frac {\beta}{2}}, \quad \tg \beta = \frac{2}{q}\sqrt{\left(\frac{p}{3}\right)^3}, \quad |\alpha| \le \frac{\pi}{4}, \quad |\beta| \le \frac{\pi}{2}.$$](https://dxdy-04.korotkov.co.uk/f/7/f/7/7f7adb478d46050b050a536c1012d33782.png)
Если

и

, то

где значения тригонометрических функций вычисляются по значению
![$$ \tg \alpha = \sqrt[3]{\tg \frac {\beta}{2}}, \quad \sin \beta = \frac{2}{q}\sqrt{\left(-\frac{p}{3}\right)^3}, \quad |\alpha| \le \frac{\pi}{4}, \quad |\beta| \le \frac{\pi}{2}.$$ $$ \tg \alpha = \sqrt[3]{\tg \frac {\beta}{2}}, \quad \sin \beta = \frac{2}{q}\sqrt{\left(-\frac{p}{3}\right)^3}, \quad |\alpha| \le \frac{\pi}{4}, \quad |\beta| \le \frac{\pi}{2}.$$](https://dxdy-03.korotkov.co.uk/f/6/f/f/6ffe359a3ce25cecfcb1bba202f5022b82.png)
Во всех трех случаях берется действительное значение кубичного корня.
Корни полного кубичного уравнения

вычисляются по формулам

где

— корни неполного кубичного уравнения.
Добавлено спустя 52 минуты 25 секунд:Корни уравнения четвертой степени. Уравнение четвертой степени

с действительными коэффициентами заменой

сводится к неполному уравнению

корни которого вычисляются по формулам:

где

— корни кубичного уравнения (
кубичной резольвенты)

и знаки перед корнями в формулах

выбираются так, чтобы выполнялось условие
 Добавлено спустя 26 минут 36 секунд:Неравенства
Добавлено спустя 26 минут 36 секунд:НеравенстваПростейшие неравенства:



Некоторые общие неравенства:

![$$\frac1n \sum_{i=1}^n a_i \ge \sqrt[n]{a_1 a_2 \ldots a_n}, a_i \ge 0$$ $$\frac1n \sum_{i=1}^n a_i \ge \sqrt[n]{a_1 a_2 \ldots a_n}, a_i \ge 0$$](https://dxdy-02.korotkov.co.uk/f/d/a/7/da7087229c173a330c1ba14a6908453882.png)
(неравенство Коши);

(неравенство Коши -- Буняковского);


(неравенство Гёльдера), где
 Добавлено спустя 21 минуту 18 секунд:Комбинаторика и бином Ньютона.
Добавлено спустя 21 минуту 18 секунд:Комбинаторика и бином Ньютона. Число перестановок из

элементов:

Число размещений из

элементов по

элементов;

Число сочетаний из

элементов по

элементов:

Формулы для числа сочетаний:



Число перестановок с повторениями (кортежами) состава (спецификации)

:

Число сочетаний из

элементов по

с повторениями:

Рекуррентная формула для числа сочетаний с повторениями:

Формула бинома Ньютона:

Формула полинома:

где суммирование проводится по всем наборам неотрицательных целых чисел

, для которых

. Коэффициенты

, вычисляемые по формуле

, называются полиномиальными коэффициентами.
Формула для числа полиномиальных коэффициентов:
