Регрессия квадратичного полинома

[Евгений Машеров]

Равенство суммы отклонений нулю не есть обязательное условие для МНК. Оно выполняется само собой ("безвозмездно, то есть даром") при включении в регрессоры столбца единиц, в других случаях вправе не выполняться.
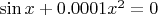
Что до решения уравнения $f(x)=0$ через минимизацию $f(x)^2$, то это оправдано, когда у нас под рукой инструмент для минимизации, а решателя уравнений отчего-то нет. Но в случае такой минимизации может быть застревание на локальных оптимумах. Решаем нечто вида $\sin x+0.0001x^2=0$, и после возведения в квадрат получаем "побочные минимумы".

[B@R5uk]

Самое забавное, что некоторые хорошие инструменты оптимизации как раз сводятся к решению системы уравнений "производная функции Лагранжа равна нулю".

[Евгений Машеров]

Ну, Ферма не только пресловутую теорему выдумал.