Некоторые участники форума (когда я прибегаю сюда с очередным вопросом) иногда жалуются на то, что им ничего не понятно. Постараюсь в этот раз разъяснить все максимально подробно, поскольку вопрос кажется мне достаточно интересным.
Пусть

это
A035506, т.е. массив (а точнее бесконечная таблица) Stolarsky читаемый по антидиагоналям. Здесь Stolarsky это фамилия некоего Kenneth B. Stolarsky.
Последовательность начинается так:

А вот так она выглядит в виде бесконечной таблицы (ниже приведен левый верхний угол):

Для разнообразия дальше можно заглянуть
сюда (одностраничный pdf на английском), но вообще это необязательно.
Итак, какова же закономерность и как, собственно, задается

? Offset (стартовый член последовательности) у
A035506 это

, но для удобства мы условимся нумеровать

по натуральным значениям

. Т.е.

,

и т.д.
Итак, пока все очень просто. Пусть

, тогда

и

. Ну а далее

.
Что примечательно, каждое натуральное число в массиве встречается ровно один раз. Т.е. сама последовательность читаемая по антидиагоналям это перестановка натуральных чисел.
Дальше нам потреюбуется PARI. Копируем прогу из соответствующей секции в
A035506 и добавляем еще кое-что:
Код:
{Stolarsky(r, c)= tau=(1+sqrt(5))/2; a=floor(r*(1+tau)-tau/2); b=round(a*tau); if(c==1, a, if(c==2, b, for(i=1, c-2, d=a+b; a=b; b=d; ); d))}
[x,y]=[1,1]; for(k=1,299, while(!(Stolarsky(x,y)==k), y++; if(Stolarsky(x,y)>k, x++; y=1)); print([x,y]); [x,y]=[1,1];);
Т.е. здесь мы ищем по каким координатам (номер строки и стоблца) у нас прячется каждое натурально число по-порядку. Выходят вот такие последовательности:
Код:
1, 2, 3, 1, 4, 2, 1, 5, 1, 3, 2, 1, 6, 1, 2, 4, 1, 3, 2, 1
1, 1, 1, 2, 1, 2, 3, 1, 4, 2, 3, 5, 1, 6, 4, 2, 7, 3, 5, 8
Что здесь можно заметить? Во второй последовательности каждые

(числа Фибоначчи) членов содержат числа от

до

. Как их генерить трудно сказать. С первой последовательностью вообще ничего не понятно.
Вот мы и ознакомились с

. В моем случае я о ней когда-то узнал, а потом забыл. Едем дальше.
Пусть

это
A200714, т.е. репрезентация Stolarsky читаемая в двоичной системе счисления, а затем переведенная в десятичную.
Последовательность начинается так:

Нумерация начинается с единицы, т.е.

,

и т.д.
Что же это за репрезентация такая? Пусть у нас есть две последовательности -

и

. Эти последовательности комплементарны, т.е. в совокупности они образуют последовательность натуральных чисел, но при этом каждое число принадлежит только какой-то одной из последовательностей (а следовательно встречается в совокупности ровно один раз).
Дальше мы задаем

. Т.е. у нас там как бы ноль, но на самом деле он символизирует пустоту. И вот к этой пустоте мы начинаем применять следующее правило:
- если
 , припишите к репрезентации
, припишите к репрезентации  в конце один
в конце один 
- если
 , припишите к репрезентации
, припишите к репрезентации  в конце одну
в конце одну 
Для наглядности можно заглянуть в текстовый файл из раздела ссылок в
A200714 (
вот он).
Теперь самое интересное. Пусть
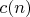
это обратная перестановка

, т.е.

.
Последовательность начинается так:

А теперь мы призываем

в качестве флешбека и шутки ради делаем следующее:
Код:
{Stolarsky(r, c)= tau=(1+sqrt(5))/2; a=floor(r*(1+tau)-tau/2); b=round(a*tau); if(c==1, a, if(c==2, b, for(i=1, c-2, d=a+b; a=b; b=d; ); d))}
a(n) = {if (n == 1, return (0)); tau = (1 + sqrt(5))/2; mn = 0; while ((m = round(mn*tau)) < n, mn++; ); if (m == n, return (2*a(mn)+1)); mn = 0; while ((m = floor(mn*(1+tau)-tau/2)) < n, mn++; ); if (m == n, return (2*a(mn))); error("neither A nor B !!"); }
c(n) = my(A=1); while(!(a(A)==n-1), A++); A
[x,y]=[1,1]; for(k=1,299, my(A=c(k)); while(!(Stolarsky(x,y)==A), y++; if(Stolarsky(x,y)>A, x++; y=1)); print([x,y]); [x,y]=[1,1];);
Т.е. мы ищем координаты натуральных чисел не в их обычном порядке, а в том, в каком они расположены в
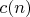
. Результат ошемляющий:
Код:
1, 1, 2, 1, 4, 2, 3, 1, 9, 4, 6, 2, 7, 3, 5, 1, 22, 9, 15, 4
1, 2, 1, 3, 1, 2, 1, 4, 1, 2, 1, 3, 1, 2, 1, 5, 1, 2, 1, 3
Иными словами, если мы вводим

(
A007814, т.е. число конечных нулей в двоичной записи

), то координаты имеют вид
 Вопросы:
Вопросы:- Если мы берем любые комплементарные последовательности, образующие в совокупности последовательность натуральных чисел и начинаем приписывать нули и единицы к пустой репрезентации, всегда ли мы будем иметь (после чтения в двоичной системе счисления и перевода в десятичную) перестановку натуральных чисел?
- Если да, то верно ли также, что аналогичная (практически) обратная перестановка проливает свет на закономерности для координат?
- Что если взять таблицу
 , такую что
, такую что  это простые, уменьшенные на единицу, а
это простые, уменьшенные на единицу, а  при
при  это простые, умноженные на
это простые, умноженные на  и результат уменьшен на единицу? Существует ли для нее репрезентация на основе комплементарности, которая дает закономерность для координат?
и результат уменьшен на единицу? Существует ли для нее репрезентация на основе комплементарности, которая дает закономерность для координат? - Уникальна ли
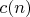 в том плане, что координаты имеют именно такой вид?
в том плане, что координаты имеют именно такой вид?
Везде подразумевается что

это не единственная последовательность, на которой базируется закономерность - ею может быть любая другая последовательность, в которой каждое натуральное число встречается бесконечное количество раз.
Благодарю вас за интерес, если вы прочитали весь пост до конца. Буду признателен за столь аналогичные (по подробности) ответы.