Здравствуйте.Путешествуя по просторам Интернета,я недавно обнаружил две любопытные публикации:
http://maxima-library.org/knigi/genre/b/524606 и
https://readli.net/tayna-kvazifaktorialnyih-chisel-kak-sushhaya-zagadka-vselennoy/.В сущности,если убрать числовой мусор,обе публикации уместятся в 2-3 предложения.По первой из них даже разгорелась дискуссия на форумах
dxdy и
math10 (см.также
https://oeis.org/search?q=A065798 ,где я увидел знакомые ники(
Someone)). Я хочу поговорить о второй. Ввиду простоты числа

в сообщениии фактически утверждалось,что числа вида

при натуральном

и

никогда("вероятно" по словам автора) не будут кратны

. Чем не задача для
PARI? Но очень скоро выяснилось,что уже число

делится на

. Более того,число из одних единичек

тоже делится.Т.о.,гипотеза автора и весь его космический "дивертисмент" оказались ложными. Ничего,бывает.Но самое интересное,что для опровержения гипотезы никакой
PARI не нужен.
Для любого простого

в последовательности

всегда найдется число,имеющее

своим делителем. Действительно,

делится на

,а при
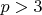
число из

единичек

делится на

ввиду малой теоремы Ферма.Не всегда надо торопиться включать комп,когда видишь вычислительную задачу.