Разделить окружность длины

на

частей отметим точками

так, чтобы для любого натурального числа

меньше

единственным образом соответствовали точки

расстояние по часовой стрелке между которыми равна

.
Например при

(

) выбрав точки так, чтобы расстояния между соседними равнялись

получаем


Имеется гипотеза, что решения при
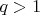
имеются только в случае, когда

является степенью простого числа. Во всяком случае это так при

. Приведу пример решения последовательных расстояний при

:
1,13,15,31,39,11,68,23,21,3,2,7,10,8,37,16,4,32,6,34.
Вот как дается количество решений (с точностью до поворотов и зеркальных отражений считающихся одинаковыми)
q 2 3 4 5 7 8 9 11 13 16 17 19
N 1 2 1 5 6 4 6 18 20 6 51 42
В связи с этим у меня возникло подозрение, что решения связаны с эллиптическими кривыми над полями из

элементов. Наверное здесь люди знают сколько "не изоморфных" эллиптических кривых над полем из

элементов. Соответствуют ли они указанной таблице?