Пусть

а также

Тогда будем иметь

Пусть

принадлежит семейству последовательностей рекуррентного типа, которые задаются следующим образом:

Здесь

это некоторые функции, такие, что

.
Теперь, собственно, к сути. Назовем последовательность


-решаемой, если для

она имеет легко задаваемую замкнутую форму типа

Здесь

это функция для верхней границы суммы,

отвечает за особенности суммирования,
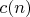
это
A059893 (в двоичной записи

реверсируем порядок всех битов кроме крайнего слева), и, наконец,

это легко задаваемые целые коэффициенты с нехитрым рекуррентным соотношением.
Например, возьмем
A002487, последовательность Штерна-Броко, и на единицу сместим точку отсчета последовательности. Тогда рекуррентное соотношение примет вид

Здесь важно отметить, что сама последовательность осталась той же, просто мы поменяли немного точку отсчета, т.е. сместили нулевый член.
Тогда будем иметь

Здесь

и

.
Другой пример - моя любимая последовательность
A329369. Она тоже оказалась

-решаемой.
Пусть

это
A007814, число конечных нулей в двоичной записи

.
Пусть

Тогда будем иметь

Здесь

это
A000120 (число единиц в двоичной записи

) а также





Существует еще две последовательности, являющиеся интерполяцией
A329369, которые тоже являются

-решаемыми - это
A341392 и
A347205. Рекуррентные соотношения для их

требуют обращения к дополнительным последовательностям. Чтобы не нагромождать уже и без того большую тему, здесь я их не привожу.
Теперь, собственно, к вопросу: имеем множество последовательностей хотя бы следующего типа

Как мы помним,

.
Вопрос: как из множества всех этих последовательностей отобрать

-решаемые? Может есть какой-то критерий, по которому с определенной вероятностью последовательность будет являться

-решаемой, что уже, собственно, будет несложно проверить? Если да, то что это за критерий (или критерии)? Можно ли получать эти критерии в процессе грубого перебора всех последовательностей? Конечно ли множество

-решаемых последовательностей или же с помощью умного перебора можно наткнуться на потенциальное бесконечное семейство?