МНК, статистика, дискретность

[B@R5uk]

B@R5uk в сообщении #1567853 писал(а):

Результат получается завышенным и мимо кассы совсем

Если взять только первые три полные ступеньки 15-16-16 (или что то же самое первые шесть), то получается больше похоже на правду:

$$a=3/(15+16+16)=3/47=0,0638\pm 0,0003$$

Оценка относительной погрешности как отношение пол пикселя к длине шести полных ступенек даёт величину большую, чем реально извлекаемая из данных погрешность.

-- 27.10.2022, 03:23 --

Теперь бы разобраться как правильно действовать, когда под скобками округления присутствует настоящая случайная величина.

[B@R5uk]

Вот пусть имеется такая простая модельная задача с зашумлённой дискретной прямой:

$$y_n=\lfloor an+b+\mathcal{N}(\sigma^2)\rfloor$$

Здесь $\mathcal{N}(\sigma^2)$ — нормально распределённая случайная величина с нулевым средним. Наглядно это выглядит как-то так:



Как действовать в этом случае?

[Евгений Машеров]

Имеем дело с ошибкой, равной сумме нормального возмущения и равномерной ошибки округления. Распределение суммы отлично от нормального, но если стандартная ошибка возмущения велика сравнительно с ошибкой округления - к нормальному близко. И можно пользоваться нормальной аппроксимацией, употребляя МНК. Главного затруднения, возникающего при использовании МНК, "тяжёлые хвосты" вызывают слишком сильные изменения в оценках, одно резко отличное значение может совершенно исказить модель - тут не будет. Таким приёмом пользуются артиллеристы (Курс Артиллерии, кн.8: Теория вероятностей, рассеивание при стрельбе. Столбошинский А.П., М.: Воениздат, 1949, § 33 - "Сложение закона Гаусса и закона равной вероятности"; полковник Столбошинский там полагает, что если параметр равномерного распределения не превышает срединной ошибки, которая приблизительно 2/3 стандартного отклонения, то можно пользоваться нормальным распределением, соответственно увеличив его дисперсию, а если превышает - надо уже считать новый закон распределения для суммы). Для последнего можно воспользоваться тем, что кумулянты n-ного порядка равномерного распределения равны $\frac {B_n} n$, где $B_n$ n-ное число Бернулли.
С практической же точки зрения - надо слушать "Валенки" использовать МНК.

[B@R5uk]

Евгений Машеров, а погрешность коэффициентов модели как рассчитывать?

[Евгений Машеров]

Я бы тупо, как в МНК (при условии, что вклад ошибки округления по сравнению с СКО шума невелик)

[B@R5uk]

Не, величина округления больше (в разы) стандартного отклонения шума. Вон даже по картинке заметно: отклонения плюс-минус один дискрет и не всегда заметны. Плюс, величину дисперсии шума я тоже не знаю, её тоже хотелось бы оценить.

[Евгений Машеров]

Если бы это была прикладная задача, притом часть большой - брал бы МНК и не парился. Но если суть именно в вероятностной модели - тут, видимо, надо строить оценку ММП, учитывающую распределение ошибки округления и нормальное, причём его дисперсия - параметр. Стоит ли усложнение возможного улучшения - не уверен.

[B@R5uk]

Евгений Машеров, задача в постановке выше прикладной не является, но она приближается к некоторой интересной для меня прикладной задаче. МНК как грубое начальное приближение, разумеется, стоит использовать, тем более, что прикладная задача нелинейная. Проблема в том, что в прикладной задаче дискреты находятся не в целых числах, а чуть-чуть смещены туда-сюда. И прикладная задача состоит в том, чтобы оценить все эти смещения (и дать оценку погрешностей этих оценок) для диапазона значений дискретов от 0 до, скажем, N. И тут без честной статистики уже никак, по-моему.

Евгений Машеров в сообщении #1568018 писал(а):

Стоит ли усложнение возможного улучшения - не уверен.

Как самостоятельная задача, на мой взгляд, она очень даже интересна. Кстати, мой подход трактовать функцию максимального правдоподобия как функцию плотности вероятности (после нормировки) обнаружить параметры модели такими-то — это, вообще, грамотный подход? Или есть что-то более логичное/удобное/теоретически обоснованное?

-- 28.10.2022, 18:53 --

Поигрался тут с МНК для данных на предыдущей картинке. Забавная ситуация получается с отклонениями экспериментальных данных от модели:



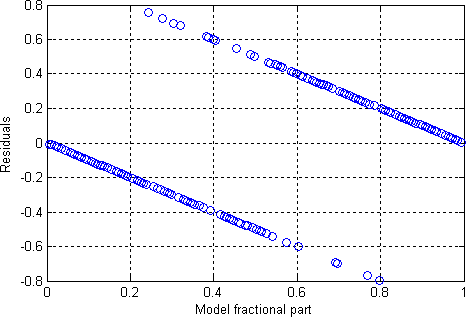
Они сильно коррелируют с дробной частью модели. В любом другом случае, при наличии такой явной корреляции с какой-либо функцией от исходных данных (например, параболическая зависимость от иксов), можно было бы утверждать, что модель неверна. Здесь же модель верна, вот только с обсчётом, видимо, что-то не то.

[B@R5uk]

Честный ММП. Модель:

$$y_n=\lfloor an+b+\mathcal{N}(\sigma^2)\rfloor$$

Если случайная величина

$$\xi\sim\mathcal{N}(\sigma^2)$$

то эта величина имеет функцию плотности вероятности

$$f(\xi)=\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{\xi^2}{2\sigma^2}\right)$$

и функцию распределения

$$F(\xi)=\frac{1}{2}+\frac{1}{2}\operatorname{erf}\left(\frac{\xi}{\sigma\sqrt{2}}\right)$$

Равенство

$$y_n=\lfloor an+b+\xi\rfloor$$

означает, что

$$y_n-an-b\le\xi<y_n-an-b+1$$

Вероятность этого равна

$$p_n=F(y_n-an-b+1)-F(y_n-an-b)=\frac{1}{2}\operatorname{erf}\left(\frac{y_n-an-b+1}{\sigma\sqrt{2}}\right)-\frac{1}{2}\operatorname{erf}\left(\frac{y_n-an-b}{\sigma\sqrt{2}}\right)$$

Если бы сигма была заметно больше единицы, то разницу двух функций можно было бы заменить производной, после чего получился бы стандартный МНК. Согласно ММП функция правдоподобия получится перемножением всех вероятностей:

$$W(a,\;b,\;\sigma)=\prod\limits_n^{}p_n=2^{-N}\prod\limits_{n=1}^{N}\left[\operatorname{erf}\left(\frac{y_n-an-b+1}{\sigma\sqrt{2}}\right)-\operatorname{erf}\left(\frac{y_n-an-b}{\sigma\sqrt{2}}\right)\right]$$

Я правильно до сего момента действовал?

-- 29.10.2022, 00:10 --

Так же вот код программы, которым предыдущий график был получен:

Используется синтаксис Matlab M

%   URL: dxdy.ru/topic151133.html
%   File: line_fit_4.m
%   Date: 2022.10.28

clc
clearvars
format compact

a = 0.21;
b = 5.73;
s = 0.2;
num = 150;

nn = (1 : num)';
%yy = floor (a * nn + s * randn (size (nn)) + b);
yy = [
     5     9    12    15    18    21    24    27    31    34
     6     9    12    15    18    21    25    28    31    34
     6     9    12    15    18    22    25    28    31    34
     6     9    13    16    19    22    25    28    31    34
     6     9    13    16    19    22    25    28    31    35
     6    10    13    16    19    22    26    29    32    35
     7    10    13    16    19    22    26    29    32    35
     7    10    13    16    19    23    26    29    32    35
     7    10    13    17    20    23    26    29    32    35
     7    11    14    16    20    23    27    29    32    35
     8    11    14    17    20    24    27    29    33    36
     7    11    14    17    20    23    27    30    33    36
     8    11    15    17    20    24    27    30    33    37
     8    11    15    18    21    24    27    30    34    37
     9    12    14    18    21    24    27    30    34    37
];
yy = yy (:);

x = [nn, ones(size (nn))] \ yy;
ym = x (1) * nn + x (2);
dy = yy - ym;
fy = mod (ym, 1);

plot (fy, dy, 'o')
grid on
xlabel ('Model fractional part')
ylabel ('Residuals')
 

[Евгений Машеров]

B@R5uk в сообщении #1568032 писал(а):

Они сильно коррелируют с дробной частью модели. В любом другом случае, при наличии такой явной корреляции с какой-либо функцией от исходных данных (например, параболическая зависимость от иксов
), можно было бы утверждать, что модель неверна. Здесь же модель верна, вот только с обсчётом, видимо, что-то не то.

Да вроде всё верно. График ошибки округления в зависимости от величины этой самой ошибки. Поскольку округляем к ближайшему - две прямые, округление вверх и вниз. Даже в чём-то тривиально.

-- 29 окт 2022, 09:12 --

Кстати, там округление или обрубание?

[B@R5uk]

Евгений Машеров в сообщении #1568104 писал(а):

Кстати, там округление или обрубание?

Округление вниз или целая часть числа, функция floor () в Матлабе (и не только в нём). На самом деле не суть важно. Одно из другого добавлением/вычитанием 1/2 получается.

Евгений Машеров в сообщении #1568104 писал(а):

две прямые, округление вверх и вниз.

На самом деле это одна прямая, потому что дробная часть числа в некотором смысле образует кольцо. При переходе из 1 в 0 или обратно эти две прямые гладко стыкуются в одну.

Евгений Машеров в сообщении #1568104 писал(а):

Да вроде всё верно.

А что на счёт формулы функции максимального правдоподобия?

$$W(a,\;b,\;\sigma)=2^{-N}\prod\limits_{n=1}^{N}\left[\operatorname{erf}\left(\frac{y_n-an-b+1}{\sigma\sqrt{2}}\right)-\operatorname{erf}\left(\frac{y_n-an-b}{\sigma\sqrt{2}}\right)\right]$$

Мне тут так видится, что в случае, когда сигма мало (в несколько раз меньше единицы), а отклонение точек от модели близко к -1/2

$$y_n-an-b\simeq-\frac{1}{2}$$

то разность функций ошибок в $p_n$ отличается от 2 где-нибудь в 4—6 знаке после запятой и при вариации искомых параметров модели (в разумных пределах) особо заметно не меняется. Другими словами, некоторые экспериментальные точки не вносят никакого вклада в значение искомых параметров. Похожая ситуация была в случае отсутствия шума: там вообще параметры модели определялись всего 4-мя точками из больше сотни. Текущая ситуация должна переходить в предыдущую при $\sigma\to 0$, по идее.

[B@R5uk]

Может, вместо квадратов в МНК какую-нибудь такую функцию использовать?

$$f\left(x,s\right)=\left\{\begin{matrix}0,&\left|x\right|\le s\\{{\left(\left|x\right|-s\right)}^2}&\left|x\right|\ge s\\ \end{matrix}\right.$$

Где параметр s подстраивается в зависимости от шага дискрета и величины шума.

А то порой сморишь на следующую картинку и понимаешь, что ну никак тут МНК не мог правильно отработать. Усреднил длинные хвосты, когда вся полезная инфа в начале.