Имеется следующее определение:
Definition (
Regular Parametric Probability Models)
Let

be a real-valued random variable, and let
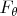
be its distribution function,
for

a parameter with parameter space
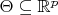
. The probability model
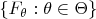
will be called regular if one of the two following conditions holds:
1. For all
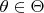
, the distribution
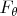
is continuous with density
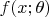
.
2. For all
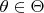
, the distribution
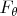
is discrete with probability mass function
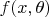
such that
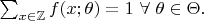
То есть такая модель
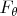
не может при одних

быть дискретной, а при других быть непрерывной.
Вопрос: есть ли в русскоязычной литературе по математической статистике аналог для такого определения? Переводить как "Регулярная вероятностная модель" или "Обычная вероятностная модель" как-то не хочется, но беглым поиском пока аналогов корректного перевода не встретил.