В курсе методов оптимизации вводится понятие аффинной размерности множества.
Так, в учебнике S. Boyd "Convex optimization" и в учебнике Васильев Ф.П. "Методы оптимизации" оно выглядит следующим образом:
Цитата:
(Аффинной) размерностью произвольного множества

называется размерность его аффинной оболочки, то есть

.
Однако, в учебнике Сухарев и др. "Курс методов оптимизации" оно несколько отличается:
Цитата:
(Аффинной) размерностью выпуклого множества

называется размерность параллельного ему линейного подпространства

(где

– произвольная точка из множества
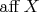
), то есть

Эти два определения несколько отличаются друг от друга, поэтому у меня возникли следующие два вопроса:
1) Верно ли, что для всякого множества

выполняется равенство

(где

– произвольная точка из множества
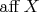
)?
Я думаю, что ответ здесь положительный (так как аффинная размерность всякого одноточечного множества  равна нулю), но не уверен полностью.
равна нулю), но не уверен полностью.2) Почему в учебнике Сухарева и др. множество

в вышеприведенном определении обязательно должно быть выпуклое? Ведь в учебниках Васильева и Boyd оно может быть произвольным.
Здесь моя догадка состоит в том, что аффинная размерность для невыпуклых множеств редко используется на практике и выглядит не очень естественно. Например, в книге Boyd указано, что аффинная размерность единичной окружности в  равна двум (так как ее аффинная оболочка есть все пространство
равна двум (так как ее аффинная оболочка есть все пространство  ), однако, как там сказано, согласно большинству других определений размерности (используемых в самых разных областях математики), единичная окружность имеет размерность 1. Как я подозреваю, исходя из подобных соображений, Сухарев в своем учебнике решил дать определение аффинной размерности только для выпуклых множеств. Но, в принципе, ничего не мешает дать это определение для произвольного множества (как это сделали Васильев и Boyd).
), однако, как там сказано, согласно большинству других определений размерности (используемых в самых разных областях математики), единичная окружность имеет размерность 1. Как я подозреваю, исходя из подобных соображений, Сухарев в своем учебнике решил дать определение аффинной размерности только для выпуклых множеств. Но, в принципе, ничего не мешает дать это определение для произвольного множества (как это сделали Васильев и Boyd).Заранее спасибо за помощь.