альтернатива при интегрировании

[mihail2102]

Уважаемые эксперты
Прошу консультации по тонкостям интегрирования. Определенный интеграл$I_{1}$изображенный ниже, имеет два выражения результата интегрирования.. Понятно, что реален только один результат. Но обосновать выбор одного из двух не получается, дифференцирование результата дает одну и ту же подынтегральную функцию. Посоветуйте обоснованный выбор. Заранее благодарен.

$I_{1}=\int\limits_{-r}^{+r}\ln(R_{1}+\sqrt{x^2+r^2+(R-r)^2})dx$
Берем по частям:$u=\ln(r+\sqrt{x^2+r^2+(R-r)^2})$

$dv=dx$

$$du=\frac{2x}{(r+\sqrt{x^2+r^2+(R-r)^2})2\sqrt{x^2+r^2+(R-r)^2}}$$

$v=x$

$$I_{1}=x\ln(r+\sqrt{x^2+r^2+(R-)^2})-\int\limits_{}^{}\frac{x^2dx}{(r+\sqrt{x^2+r^2+(R-r)^2})\sqrt{x^2+r^2+(R-r)^2}}$$

Рассмотрим вторую интегральную часть выражения $I_{1}$

$$(-1)\int\limits_{-r}^{+r}\frac{x^2dx}{(r+\sqrt{x^2+r^2+(R-r)^2})\sqrt{x^2+r^2+(R-r)^2}}$$

Введем переменную $t$:

$$t=\sqrt{x^2+r^2+(R-r)^2}$$

$$dt=\frac{2xdx}{2\sqrt{x^2+r^2+(R-r)^2}}$$

$$ x=\sqrt{t^2-r^2-(R-r)^2}$$

,
то в новых переменных интеграл будет иметь вид:

$$ (-1)\int\limits_{}^{}\frac{\sqrt{t^2-r^2-(R-r)^2}dt}{(r+t)}$$

Введем новую переменную: $(r+t)=m $,$t=m-r$.
Тогда интеграл будет иметь вид:

$$(-1)\int\limits_{}^{}\frac{\sqrt{(m-r)^2-r^2-(R-r)^2}dm}{m}=(-1)\int\limits_{}^{}\frac{\sqrt{m^2-2mr+r^2-(R-r)^2}dm}{m}$$

$$=(-1)\int\limits_{}^{}\frac{\sqrt{m^2-2rm-(R-r)^2}dm}{m}$$

коэффициенты квадратного трехчлена под корнем равны:
$ a=1, b=-2r, c=-(R-r)^2$
Согласно таблицам интегралов (Двайт) 380.311

$$(-1)\int\limits_{}^{}\frac{\sqrt{am^2+bm+c}dm}{m}=(-1)(\sqrt{am^2+bm+c}+b/2\int\limits_{}^{}\frac{dm}{\sqrt{am^2+bm+c}}+c\int\limits_{}^{}\frac{dm}{m\sqrt{am^2+bm+c}})$$

Это равно:

$$(-1)(\sqrt{m^2-2rm-(R-r)^2}+(-r)\int\limits_{}^{}\frac{dm}{\sqrt{m^2-2r-(R-r)^2}}+(-(R-r)^2)\int\limits_{}^{}\frac{dm}{m\sqrt{m^2-2rm-(R-r)^2}})\eqno (1)$$

Согласно таблицам(Двайт) 380.001

$$\int\limits_{}^{}\frac{dm}{\sqrt{am^2+bm+c}}=\frac{1}{a^\frac{1}{2}}\ln|(2\sqrt{(a(am^2+bm+c))}+2am+b)|$$

$a\geqslant0$
Для реальных $a,b,c$ интеграл будет иметь вид:

$$\int\limits_{}^{}\frac{dm}{\sqrt{m^2-2rm-(R-r)^2}}=\ln(2\sqrt{m^2-2rm-(R-r)^2}+2m-2r)$$

Следующий интеграл согласно таблицам(Двайт) 380.111

$$\int\limits_{}^{}\frac{dm}{m\sqrt{am^2+bm+c}}=\frac{1}{\sqrt{-c}}\arcsin(\frac{bm+2c}{|m|\sqrt{b^2-4ac}})\eqno (1,2)$$

Для реальных $a,b,c$ интеграл будет иметь вид:

$$\frac{1}{\sqrt{-(-(R-r)^2)}}\arcsin\frac{-2rm+2(-(R-r)^2)}{m\sqrt{4r^2-4(-(R-r)^2})}$$

$$=\frac{1}{(R-r)}\arcsin\frac{-2rm-2(R-r)^2}{m\sqrt{4r^2+4(R-r)^2}}$$

В этом интеграле возвращаемся к переменной $ t=m-r, m=t+r$

$$\frac{1}{(R-r)}\arcsin\frac{-2r(t+r)-2(R-r)^2}{(t+r)\sqrt{4r^2+4(R-r)^2}}$$

Переходим к переменной (х) при $ t=\sqrt{x^2+r^2+(R-r)^2}$

$$\frac{1}{(R-r)}\arcsin\frac{-2r(r+\sqrt{x^2+r^2+(R-r)^2})-2(R-r)^2}{(r+\sqrt{x^2+r^2+(R-r)^2})\sqrt{4r^2+4(R-r)^2}}$$

Собираем выражение (1):
$(-1)(\sqrt{m^2-2rm-(R-r)^2}-r\ln(2\sqrt{m^2-2rm-(R-r)^2})+2m-2r)-(R-r)\arcsin\frac{-2r(r+\sqrt{x^2+r^2+(R-r)^2)}-2(R-r)^2}{(r+\sqrt{x^2+r^2+(R-r)^2})\sqrt{4r^2+4(R-r)^2}}\eqno (2)$
Возвращаемся к переменной х в первых двух слагаемых:
$m=t+r=\sqrt{x^2+r^2+(R-r)^2}+r$
тогда

$$\sqrt{m^2-2rm-(R-r)^2}=$$

$$=\sqrt{x^2+r^2+(R-r)^2+2r\sqrt{x^2+r^2+(R-r)^2}+r^2-2r(\sqrt{x^2+r^2+(R-r)^2$$

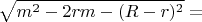
далее продолжение общего корня $\sqrt{-(R-r)^2}=$$=\sqrt{x^2+2r^2-2r^2}=x$
Тогда общий вид выражения (2) в переменных (х) будет иметь вид:
$(-1)(x-r\ln(2x+2(r+\sqrt{x^2+r^2+(R-r)^2})-2r)-(R-r)\arcsin\frac{-2r(r+\sqrt{x^2+r^2+(R-r)^2})-2(R-r)^2}{(r+\sqrt{x^2+r^2+(R-r)^2})\sqrt{4r^2+4(R-r)^2}})\eqno (3)$
Возвращаемся к выражению $I_{1}$, при интегрировании по частям и добавляем к полученному выше свободное выражение. Таким образом общий вид $I_{1}$ в переменной (х) будет иметь вид:
$ I_{1}=x\ln(r+\sqrt{x^2+r^2+(R-r)^2})-x+r\ln(2x+2\sqrt{x^2+r^2+(R-r)^2})+(R-r)\arcsin\frac{-2r(r+\sqrt{x^2+r^2+(R-r)^2})-2(R-r)^2}{(r+\sqrt{x^2+r^2+(R-r)^2})\sqrt{4r^2+4(R-r)^2}}$
При подстановке пределов интегрирования $x=+r, x=-r$ арксинус сокращается.
Но арксинус в выражении (3) получен из табличного интеграла 380.111(Двайт), это выражение (1.2). Имеется и другое представление этого интеграла (Прудников А.П. Брычков, Маричев. интегралы и ряды. 1981 ... стр 103 №26), Причем в таблицах интегралов Двайта, нет результата интегрирования с арктангенсом:

$$\int\limits_{}^{}\frac{dm}{m\sqrt{am^2+bm+c}}=\frac{1}{\sqrt{-c}}\arctg\frac{bm+2c}{2\sqrt{-c}\sqrt{am^2+bm+c}}$$

При $a=1, b=-2r, c=-(R-r)^2$этот интеграл будет иметь вид;
$\int\limits_{}^{}\frac{dm}{m\sqrt{m^2-2rm-(R-r)^2}}=\frac{1}{(R-r)}\arctg\frac{-2rm-2(R-r)^2}{2(R-r)\sqrt{m^2-2rm-(R-r)^2}}$
В переменной (х) этот интеграл будет иметь вид:

$$\frac{1}{(R-r)}\arctg\frac{-2r(r+\sqrt{x^2+r^2+(R-r)^2})}{2(R-r)x}$$

Альтернативное выражение для$ I_{1}$ будет иметь вид:
$ I_{1}=x\ln(r+\sqrt{x^2+r^2+(R-r)^2})-x+r\ln(2x+2\sqrt{x^2+r^2+(R-r)^2})+(R-r)\arctg\frac{-2r(r+\sqrt{x^2+r^2+(R-r)^2})-2(R-r)^2}{2(R-r)x}$
При подстановки пределов интегрирования $x=+r, x=-r $ арктангенс не сокращается
Получаются два разных результата интегрирования одного и того же интеграла.

[Otta]

И откуда там быть арктангенсу?
Все остальное просто не смотрела. Вы пишете много лишнего, суть проблемы можно было изложить короче.

[worm2]

Насколько я понял, нужно доказать (либо опровергнуть), что

$$\arcsin\frac{-2r(r+\sqrt{x^2+r^2+(R-r)^2})-2(R-r)^2}{(r+\sqrt{x^2+r^2+(R-r)^2})\sqrt{4r^2+4(R-r)^2}} \equiv \arctg\frac{-2r(r+\sqrt{x^2+r^2+(R-r)^2})-2(R-r)^2}{2(R-r)x}.$$

Я слишком стар, чтобы делать это вручную, поэтому привлёк Mathematica.
Она подтвердила, что тождество верное.

-- Чт сен 15, 2022 12:02:31 --

Точнее, я немного другое доказывал, вот код:

Используется синтаксис Matlab M

Clear[A];
Clear[B];
Clear[F];
A[x_, r_, R_] = -2 r (r + Sqrt[x^2 + r^2 + (R - r)^2]) - 2 (R - r)^2;
B[x_, r_, R_] = 2 (R - r) x;
F[x_, r_, R_] = (r + Sqrt[x^2 + r^2 + (R - r)^2]) Sqrt[4 r^2 + 4 (R - r)^2];
Simplify[F[x, r, R]^2 - A[x, r, R]^2 - B[x, r, R]^2]
 

Результат: 0.
Пользовался тождеством:

$$\arctg\frac AB\equiv\arcsin\frac {A}{\sqrt{A^2+B^2}}.$$

[Евгений Машеров]

(Оффтоп)

"Только наш бледнолицый брат способен дважды наступить на одни грабли"...
topic146359.html

[Sinoid]

mihail2102 в сообщении #1564695 писал(а):

Понятно, что реален только один результат.

Кто сказал? Например, когда я прорешивал задачник Бермана, т при решении по как раз интегрирования в некоторых задачах как раз с обратными триг. функциями удавалось брать какой-нибудь интеграл двумя различными подстановками. Получалось 2 различных выражения, отличающиеся друг от друга, понятно, на константу. Я их приравнивал, находил константу, получал неизвестное мне соотношение. Было интересно...

[mihaild]

Sinoid в сообщении #1564713 писал(а):

Кто сказал?

Определение определенного интеграла.

[Sinoid]

mihaild
А, ну численно-то да. Нет, я имел ввиду выражения.

[mihaild]

Sinoid в сообщении #1564724 писал(а):

А, ну численно-то да. Нет, я имел ввиду выражения.

Что "численно"? Задача - найти определенный интеграл. Это число. Соответственно если мы получили два способа записать ответ, то они должны обозначать одно и то же число (а не два отличающихся на ненулевую константу).

[Евгений Машеров]

Ну, если Вам надо число, то и получите число. Подставьте в обе Ваши формулы какие-нибудь значения и посчитайте. Если совпадёт - а Вы не поверите - то подставьте что-то иное и посчитайте.

(Оффтоп)

Втирать до полного удовлетворения.

[Sinoid]

mihaild в сообщении #1564725 писал(а):

Задача - найти определенный интеграл. Это число.

Ну, если так подходить, то, вообще говоря, получится, скорее всего, и никакое не число, а выражение, скорее всего, с двумя переменными, хотя, да, они могут чисто случайным образом уйти. Но это будет чистое везение, как вы понимаете. Это во-первых. Во-вторых, судя по стартовому посту темы, ТС беспокоит именно не их несовпадение по выражениям их после подстановок пределов с вычислением, представлением в численном виде того, что можно вычислить и представить - иначе после такого вычисления он тем или иным способом пришел бы к совпадению этого. Нет, его волнует несовпадение до этого. И, упомянув, какие несовпадения получал я, я лишь хотел показать, что так бывает, хотя да, аналогия лишь отчасти.

[mihaild]

Sinoid в сообщении #1564752 писал(а):

ТС беспокоит именно не их несовпадение по выражениям их после подстановок пределов с вычислением, представлением в численном виде того, что можно вычислить и представить - иначе после такого вычисления он тем или иным способом пришел бы к совпадению этого

Насколько я понял, ТС беспокоило именно то, что получившиеся выражения оказались разными как функции от $r$.

[Sinoid]

mihaild в сообщении #1564755 писал(а):

Насколько я понял, ТС беспокоило именно то, что получившиеся выражения оказались разными как функции от

Так и я о том же. Но в несовпадающих выражениях-то не были заменены хотя бы те части, коэффициенты, которые могут быть заменены своими приближенными своими значениями в десятичной позиционной системе для оценки для себя, равны выражения или нет, стоит или нет тратить усилия для доказательства равенства этих выражений. Разумеется, в доказательстве эти приближенные значения никак не должны фигурировать. Это так, для прощупывания, внутреннего уяснения, доказывающему.

[Евгений Машеров]

Да причём тут приближения?

(Оффтоп)

Поправляя фуражку прапорщика Ясненько, старшины роты к-на Очевидность.

Тангенс это отношение катетов, синус - катета к гипотенузе. Квадрат гипотенузы есть сумма квадратов катетов. То есть один и тот же угол можно выразить двумя разно выглядящими формулами. Но они тождественны. Никакого противоречия нет. Это не два разных, а два по-разному записанные выражения. Не знаю, хватит ли мне трудолюбия расписать знаменатель $\sqrt{A^2+B^2}$ вручную, тем более что уже это сделали выше машинно. Но более чем уверен, что после нудных выкладок получим
$\arctg\frac AB\equiv\arcsin\frac {A}{\sqrt{A^2+B^2}}$

[mihail2102]

Еще раз благодарю уважаемых экспертов за разъяснения.
Я понял так, что части интеграла с арктангенсом и арксинусом, суть побочный нейтральный элемент интегрирования, тождественно равный нулю.
Обнуление арктангенса и арксинуса в вышеприведенном интеграле впоследствии приводит к закономерному отношению гравитационного поля шара к полю куба одинаковых размеров и массы на бесконечности, равного 0.5
Мультипольное разложение поля куба и поля шара, показывает, что отношение этих полей на бесконечности равно 1(единица).Поскольку величина 0.5 была получена при помощи интегрирования полей шара и куба и оценки отношения этих полей на бесконечности, противоречит величине отношения при мультипольном разложении равном 1 (единица), то я делаю вывод, что проверка интегрального исчисления на непрерывных множествах, самим интегральным исчислением противоречива по своей сути и не может применяться на практике. Вот это утверждение может иметь место или нет?.

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Пургаторий (М)»
Причина переноса: чего и следовало ожидать.

-- 17.09.2022, 15:59 --

mihail2102, бан на месяц за очередное возобновление темы из Пургатория и систематическую невменяемость.