Вопрос возник из крайне любительских рассуждений на тему пентадекатлона. Но там спрашивать стесняюсь

Может ли число вида

иметь ровно 6 делителей?
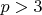
— простое.
Натурный эксперимент в PARI/GP в диапазоне до

кроме числа

ничего не обнаружил.
Рассуждения:

. Один из сомножителей обязательно делится на

. Так как делителей

, то возможны паттерны

и

.
Есть также подозрение, что для нечётных

число

не может иметь шесть делителей, либо

.
Наверное, вопрос простой, но от жары.......