все точки обода колеса

имеют скорость

Это неверно.
В СО, связанной с тележкой, все точки обода колеса имеют одну и ту же скорость по модулю. Но она не равна

.
В СО, связанной с горизонтальной плоскостью, разные точки обода колеса имеют разные по модулю скорости.
Кроме того, Вы неверно представляете себе поле скоростей колеса.
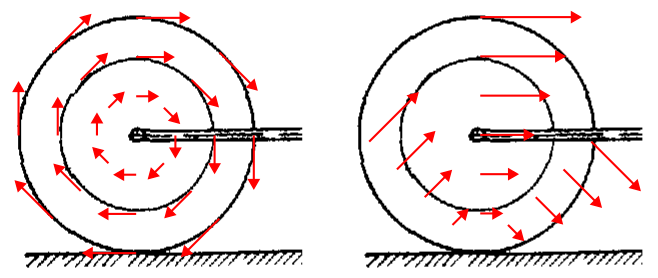
В СО, связанной с тележкой, поле скоростей выглядит как на левой картинке (каждая стрелка относится к точке колеса, совпадающей с её началом). Но в этой системе МЦС — не точка соприкосновения колеса с плоскостью, а центр колеса (что и видно из картинки).
В СО, связанной с плоскостью, поле скоростей как на правой картинке. Здесь МЦС — точка соприкосновения колеса с плоскостью. Но скорость нижней точки обода направлена не влево, как Вы изобразили, а вправо.